- ファイナンシャルフィールド（コラム掲載）
- ハピママ（マネー系コラム掲載）
SPI非言語の「物の流れと比率」は、図で示された人や物の流れを参照して、正しい式や割合、数量を求める問題です。コツさえつかめば得点を獲得しやすい単元ですが、少し癖のある特殊な出題形式なので慣れが肝心になります。
この記事では、非言語領域を得意とする山田さんとともにSPIの「物の流れと比率」の解き方について解説していきます。出題傾向としては、おもにペーパーテストで見られる単元ですが、出題傾向が変わる可能性もあるので、ほかの形式で受験予定の人もしっかり対策をしておきましょう。
記事の後半には練習問題を3問用意しています。演習を積んで解き方のコツをつかんでくださいね。
よりSPIの本番をイメージして対策したい人は、SPI対策模試にも挑戦してみてください。
SPI「物の流れと比率」の概要
- 問題パターン：図を表す正しい式を選ぶ問題、式をたどって数を求める問題、到着する割合を求める問題
- 1問あたりの時間：1分程度
- 形式ごとの出題頻度：テストセンター（出題無し）ペーパーテスト（中）Webテスティング（出題無し）
- 物の流れと比率を解くときのコツをわかりやすく教えてください！
頭の中だけで解かずにメモをとって整理しよう
「物の流れと比率」は、計算の難易度はそれほど高くないものの、図を読み取って数字を整理していく能力が問われます。
図がある場合は、問題文で示された数字を確認しながら書き込んでいき、一つひとつ整理していきましょう。
分岐や合流が起きる場所は特に要注意で、頭の中だけで整理しようとするのは危険です。必ずメモをとって、ケアレスミスを防ぐようにしてください。
「物の流れと比率」の問題に共通する前提条件
「物の流れと比率」の問題には必ず以下のような前提条件が提示されます。
前提条件①
以下の図は、業者Xの取扱製品のうち、割合pが業者Yへ供給されることを示している。
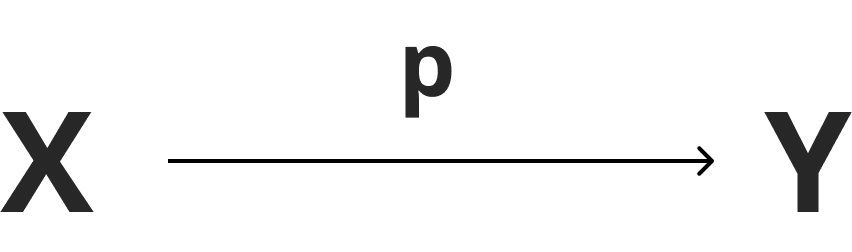
ここで、各業者が扱う製品量をそれぞれX,Yと定義すると、両者の関係は数式Y=pXで表される。
前提条件②
以下の図は業者Xから割合p、業者Yから割合qがそれぞれ業者Zへ供給されることを示している。
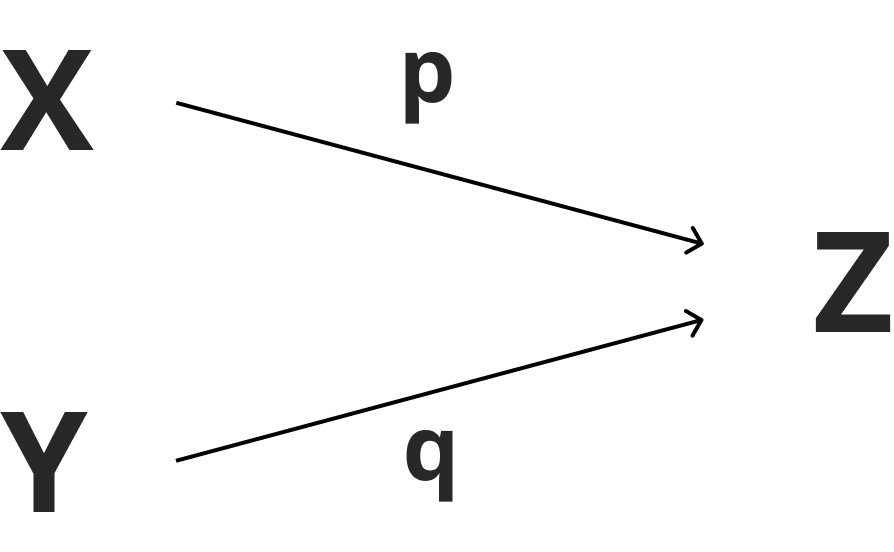
このとき、三者の関係は「Z=pX+qY」で表される。
前提条件③
以下の図は業者Xから業者Yへ割合pで供給され、そこからさらに割合qが業者Zへ供給されることを表している。
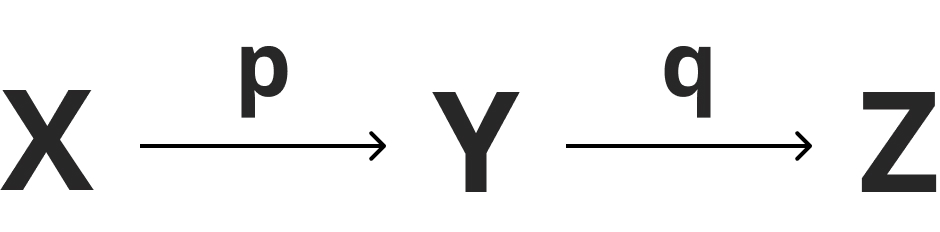
このとき、三者の関係は「Z=qY」あるいは「Z=q（pX）=pqX」で表される。
なお、式については次のような一般の演算
（p+q）X=pX+qX
r（p+q）X=prX+qrX
などが成り立つものとする。
SPI「物の流れと比率」練習問題3問｜山田さんによる解き方の解説付き！
ここからは、SPI 非言語 「物の流れと比率」の練習問題を専門家の解説とともに3問紹介します。さまざまな問題パターンを紹介しているので、最後まで解いて「物の流れと比率」を完璧にしていきましょう。
また今回「物の流れと比率」を初めて解くという人は、「問題を解く前に確認！ 物の流れと比率の解答のコツ」を読み、ポイントを押さえてから取り掛かるようにしてください。
問題1（難易度：★★☆☆☆）
問題
“「物の流れと比率」の問題に共通する前提条件”で提示した前提にもとづき、以下の各設問に答えよ。
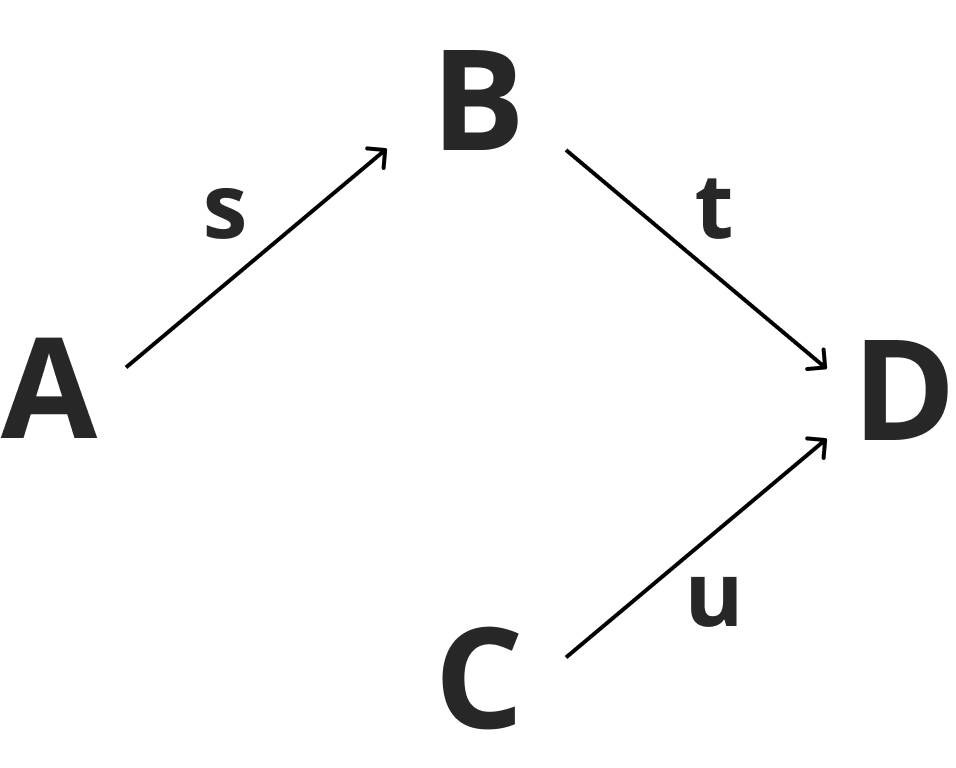
上の図は3つの業者A、B、Cから業者Dへの製品供給ルートを表している。このとき、Dに供給される量を表す数式として、正しいものはどれか。
選択肢
正解：A
図の流れを整理する。Dへ到達するルートは2つある。
1つ目は、AからBを経由してくるルートである。AからBへの流れはB=sAなので、BからDへの流れはtB=t(sA)=stAとなる。
2つ目は、Cから直接Dへ入るルートであり、これはuCと表せる。
Dではこれらが合流するため、両方を足し合わせる。
したがって、正しい数式はD=stA+uCである。
「物の流れと比率」は、学校で習う数学とはかなり特徴が異なるので、独自の感覚を身に付ける必要があります。
この問題であれば、Bは物を供給するのでなく、一定の係数（t）をかけてAから供給された物を素通りさせる、という理解になることを押さえましょう。
問題2（難易度：★★★☆☆）
問題
“「物の流れと比率」の問題に共通する前提条件”で提示した前提にもとづき、以下の各設問に答えよ。
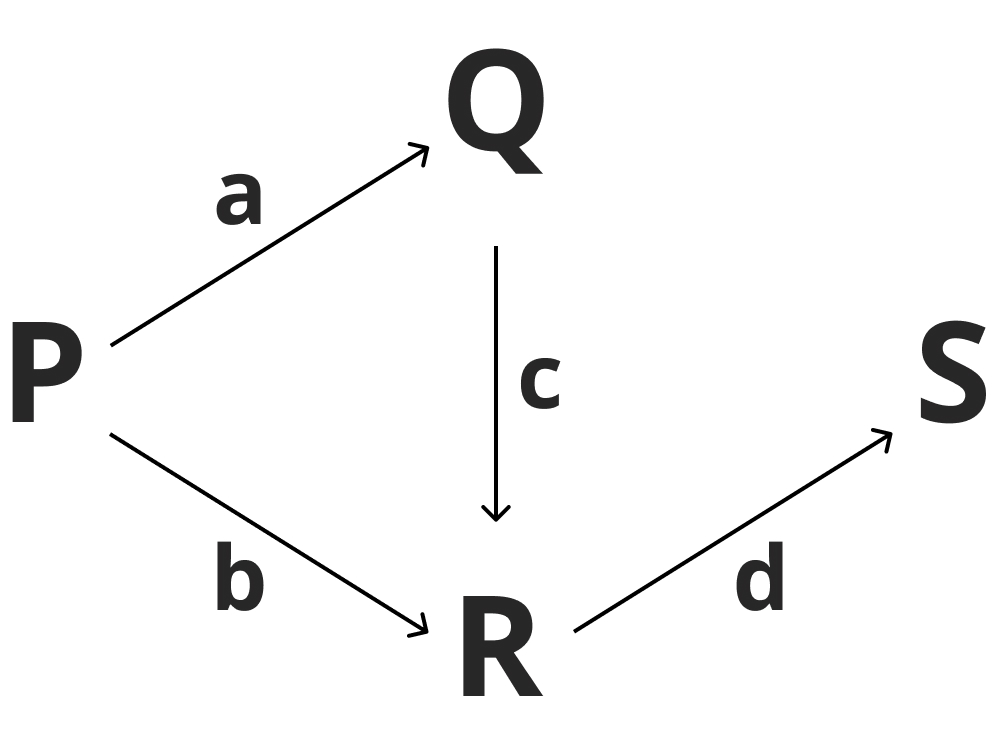
上の図は業者Pから業者Sに商品が供給されるまでの流れを示している。a＝0.3、b＝0.2、c＝0.4、d＝0.5である。このとき、PからQとRに出荷された製品の総量のうち、最終的にSに納品される量は何％か。
選択肢
正解：C
Pから出荷された総量と、Sに納品される量の比率を求める。
Pからの出荷総量は、QへのaP=0.3Pと、RへのbP=0.2P、合計で0.5Pとなる。
Sへの納品量を考える際には、Rへの納品ルートが2つあることを考慮する必要がある。1つ目はPからRへ直接行くルートで、その量はbP=0.2P。2つ目はQを経由してRへ行くルートで、その量はcQ=c(aP)=0.4(0.3P)=0.12P。Rはこれらを合計した値なのでR=0.32Pであり、Sへの納品量S=dRより、S=0.5×0.32P=0.16Pである。
求める割合は、0.16Pを0.5Pで割って算出する。0.16P÷0.5P＝0.32 よって、正解は32％である。
問題3（難易度：★★★★☆）
問題
“「物の流れと比率」の問題に共通する前提条件”で提示した前提にもとづき、以下の各設問に答えよ。
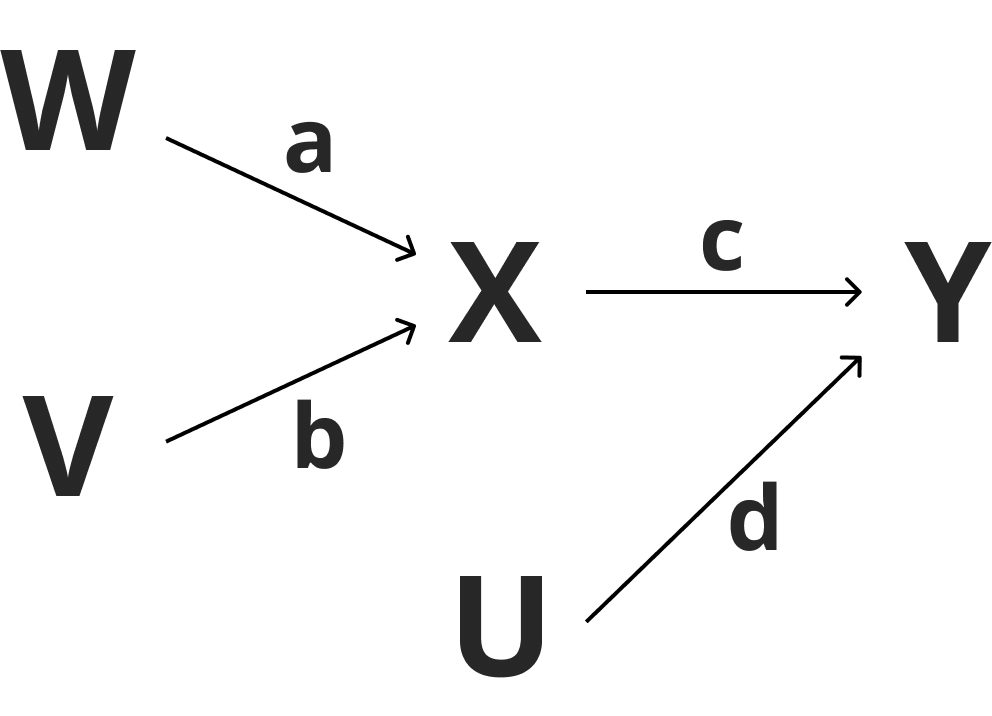
上の図は4つの業者U、V、W、Xから業者Yへの製品供給ルートを表している。a=0.5、b=0.4、c=0.6、d=0.2である。業者Wの在庫数が120、業者Uの在庫数が200、業者Yに集まった数が124のとき、業者Vの在庫数はいくつか。
選択肢
正解：C
まず、業者Xに集まる数を式で表す。X=aW+bVである。
次に、最終地点Yに集まる数を式で表す。Y=cX+dUである。
このYの式のXに、最初の式を代入すると、Y=c(aW+bV)+dUとなる。
数値を代入してVを求める。124=0.6{(0.5×120)+0.4V}+(0.2×200)
124=0.6(60+0.4V)+40
かっこの外の40を移項して、84=0.6(60+0.4V)
両辺を0.6で割ると、140=60+0.4V、0.4V=80、V=200
したがって、業者Vの在庫数は200である。
非常に内容が混みいった問題なので、問題文で示された数字を図に実際に書き込み、一つひとつ整理していくことが重要です。
最終的に製品が集まるのはY（124）ですが、その数値は数式で表すと
Y=cX+dU=c(aW+bV)+dU
となりますね。
上記の式のうちV以外の数字はすべて示されているので、あとは1次方程式として確実に計算しましょう。
SPI「物の流れと比率」を対策する際のポイント
SPIの非言語に関する記事
◇非言語の対策
SPI非言語は対策すれば怖くない！ 出題傾向や例題を徹底解説
SPIに関する記事
◇解答時間
SPIの解答時間を受検方式別に解説！ 時間切れを防ぐコツ10選も
◇勉強法
効率抜群なSPIの勉強法｜出題形式と頻出問題を踏まえた対策を伝授
◇勉強時間
SPIの勉強時間をプロが解説！ おすすめの進め方や重点ポイントも
物の流れと比率以外の練習問題も解いてみよう！
SPIは多くの分野に分かれています。練習問題を繰り返し解いて、苦手を攻略しましょう。
各分野の問題が解けたら、最後にSPI模試に挑戦してみましょう。
執筆・編集 PORTキャリア編集部
明日から使える就活ノウハウ情報をテーマに、履歴書・志望動機といった書類の作成方法や面接やグループワークなどの選考対策の方法など、多様な選択肢や答えを提示することで、一人ひとりの就活生の意思決定に役立つことを目指しています。 国家資格を保有するキャリアコンサルタントや、現役キャリアアドバイザーら専門家監修のもと、最高品質の記事を配信しています。
＞ コンテンツポリシー
記事の編集責任者 熊野 公俊 Kumano Masatoshi
高校卒業後、航空自衛隊に入隊。4年間の在籍後、22歳で都内の大学に入学し、心理学・教育学を学ぶ。卒業後は人材サービスを展開するパソナで、人材派遣営業やグローバル人材の採用支援、女性活躍推進事業に従事。NPO（非営利団体）での勤務を経て、「PORTキャリア」を運営するポートに入社。キャリアアドバイザーとして年間400人と面談し、延べ2500人にも及ぶ学生を支援。2020年、厚生労働大臣認定のキャリアコンサルタント養成講習であるGCDF-Japan（キャリアカウンセラートレーニングプログラム）を修了
アドバイザーのリアル・アドバイス！慌てずにまずは図に数字を書き込んで整理しよう
国家資格キャリアコンサルタント／2級ファイナンシャル・プランニング技能士
山田 圭佑
プロフィールを見るこの単元は計算は複雑ではないものの、図を用いて状況を整理する力が求められます。できる限り素早く回答したいと思っても、まずは図に数字を書き込んで整理する時間を確実に取ることをおすすめします。
重要なことは
①問題文で与えられた情報を確実に読み取り、図に書き込むこと
②数式で整理していくこと
の2つです。私の場合は、図に数字を書き込む→その内容を確認しながら数式に落とし込む→最終的な正答を導く計算をするという手順でおこないます。
提示されていない情報もメモで補う訓練が大切
この項目は中学・高校で習う数学とはかなり色合いが異なるため、高得点を取るためには独自の練習が必要になるでしょう。読み取った情報をメモなどを用いて確実に整理できるようにする訓練をしてください。
特に「分岐や合流」がある地点は要注意です。たとえば「Aのコースに30%が流れた」と問題文に書かれていた場合、「残りの70%は別のコースに流れた」という情報を自分で補いながら図を書きましょう。