・すぐに問題を解きたい人は練習問題35問をチェック
・まずは解き方から知りたい人は「解き方のコツ」をチェック
SPIの「場合の数」は非言語分野で出題されます。基本的な公式は「順列」と「組み合わせ」の二つです。問題文からどちらの公式を使うべきかを適切に汲み取る力が求められます。
この記事では、Webテストの講師をしていた経験を持つキャリアコンサルタントの小寺さんとともにSPIの「場合の数」の解き方について解説していきます。具体的な対策方法についても解説しているので、「場合の数」に苦手意識がある人は参考にしてみてください。
記事の後半では「場合の数」の練習問題を35問紹介しています。公式を覚えるだけでなく実際に手を動かして解くことで、確実に得点力がアップします。ぜひ最後まで確認してみてくださいね。
よりSPIの本番をイメージして対策したい人は、SPI対策模試にも挑戦してみてください。
問題を解く前に確認! 場合の数の解答のコツ
SPI「場合の数」の概要
- 問題パターン:順列、組み合わせ、余事象、色塗りなど
- 1問あたりの時間:40秒~1分程度
- 形式ごとの出題頻度:テストセンター(中)ペーパーテスト(中)Webテスティング(大)
- 場合の数の解答のコツを教えてください
3つのチェック項目を意識して解くクセをつけよう!
場合の数は、SPI非言語の中でも頻出かつ差がつきやすい分野です。一見何となく解けそうな問題でも実は数え間違えがあったりと、時間もミスも一気に増えやすい強敵と言えるでしょう。
まず意識したいのは、
①「順番を区別するか(順列)/しないか(組合せ)」
②「同じものを何度も使えるか」
③「条件は少なくとも◯なのか」
の3点です。
問題を読むときに、この3つをメモレベルで整理してから式を立てるクセをつけましょう。1問あたりの目安時間は、標準問題で40〜60秒、やや重い条件付きでも90秒以内を意識し、立式までのスピードを重点的に鍛えると効果的です。
絶対に覚えておきたい! 場合の数の公式の使い分け
「場合の数」を解くうえで必須の公式を紹介します。忘れてしまっている人はこちらを参考にして、問題に取り組みましょう。
場合の数の公式
- 順列:nPr
- 円順列:(n – 1)!
- 組み合わせ:nCr
- 重複順列:nのr乗
SPI「場合の数」の練習問題35問|小寺さんによる解説付き
SPI「場合の数」の練習問題を解説付きで35問紹介します。基礎的な問題から、実際の試験で頻出する一歩進んだ応用問題まで、網羅的に紹介しています。ぜひ最後まで解いて、解法のパターンを体に定着させましょう。
また今回初めて「場合の数」に挑戦するという人は、「問題を解く前に確認! 場合の数の解答のコツ」を読んでから問題に移ることをおすすめします。
問題1(難易度:★☆☆☆☆)
問題
以下の問いについて、その組み合わせや並び方が何通りあるか答えなさい。
サークル活動において、メンバーのA、B、C、Dの4人の中から、話し合いの「司会」と「書記」を1名ずつ選出することになった。兼任は認めないものとする場合、この2名の選び方は何通りあるか。
選択肢
正解:C
司会と書記という役割(区別)があるため、組み合わせではなく順列の考え方を用いる。
4人の中から異なる2人を選んで並べる計算となる。
まず、司会の選び方は4人の候補がいるため4通り。
次に書記は、司会に選ばれた1人を除く残りの3人から選ぶため3通りとなる。
これらを掛け合わせることで答えが求まる。
4×3=12よって、12通りである。
問題2(難易度:★☆☆☆☆)
問題
以下の問いについて、その組み合わせが何通りあるか答えなさい。
ジェラート店に4種類の異なるフレーバー(バニラ、チョコ、ストロベリー、抹茶)がある。この中から異なる2種類を選んでダブルを注文する場合、フレーバーの組み合わせは何通りあるか。
選択肢
正解:B
選ぶ2種類のフレーバーに順序や役割の区別はないため、「組み合わせ」の考え方を用いる。
4種類の中から2つを選ぶ計算(4C2)となる。
計算式は、4×3を2×1で割ることで求められる。
(4×3)÷(2×1)=12÷2=6
よって、6通りである。
ちなみに、「バニラ・チョコ」と「チョコ・バニラ」は同じ組み合わせとして扱う点に注意する。
問題3(難易度:★☆☆☆☆)
問題
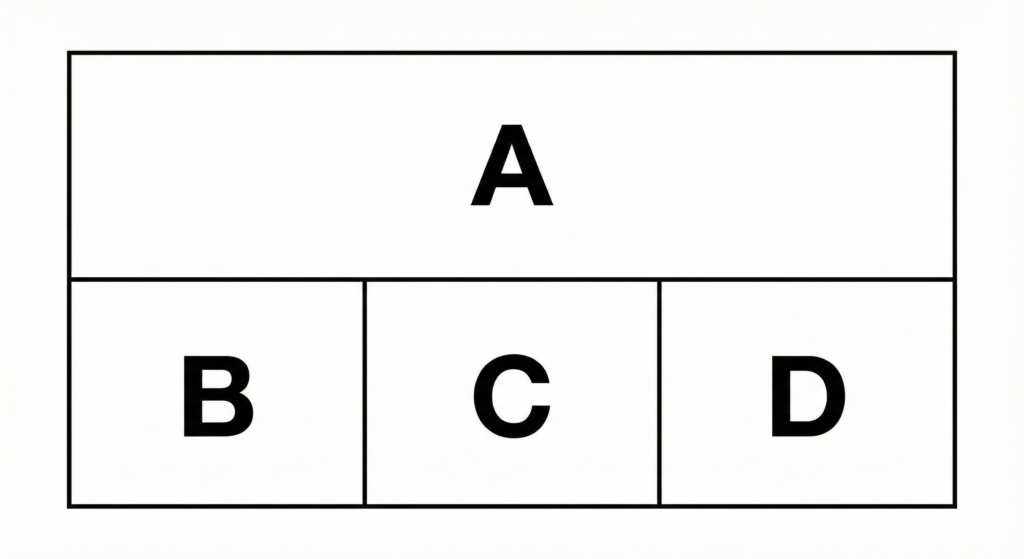
画像のように、長方形が4つの領域(上部のA、下部左のB、下部中央のC、下部右のD)に区分けされている。これらの領域を指定された数の色を使って塗り分ける。ただし、隣り合う領域には異なる色を使わなければならない。
この4つの領域を、赤・青・緑・黄の「4色」すべてを使って塗り分ける場合、塗り方は何通りあるか。
選択肢
正解:A
隣接数の多いAとCから順に決定していく基本的なパターンである。
Aの色:4色から自由に選べる(4通り)。
Cの色:Aと隣り合うため、A以外の色から選ぶ(3通り)。
Bの色:A、Cと隣り合う。AとCは色が異なるため、残りの2色から選ぶ(2通り)。
Dの色:4色すべてを使って塗るので、残りの1色を使用する(1通り)。
これらを掛け合わせる。4×3×2×1=24よって、24通りである。
問題4(難易度:★★☆☆☆)
問題
以下の問いについて、その組み合わせや並び方が何通りあるか答えなさい。
ある旅行代理店が、6つの観光地(A〜F)をリストアップした。この中から3カ所を選び、「1日目」「2日目」「3日目」にそれぞれ1カ所ずつ訪れるツアーを企画する場合、観光地の選び方と回る順番のパターンは何通りあるか。
選択肢
正解:C
日程(1日目~3日目)によって訪れる場所が区別されるため、順列として計算する。
6つの観光地から3つを選んで順番に並べる。
1日目の選び方は6通り。
2日目は、残りの5カ所から選ぶので5通り。
3日目は、残りの4カ所から選ぶので4通り。
これらを順に掛け合わせる。
6×5×4=120
よって、120通りである。
問題5(難易度:★★☆☆☆)
問題
以下の問いについて、その組み合わせや並び方が何通りあるか答えなさい。
陸上競技の決勝戦に7人の選手が出場した。この中から、金メダル(1位)、銀メダル(2位)、銅メダル(3位)の獲得者を予想する場合、その組み合わせは何通りあるか。ただし、同着はないものとする。
選択肢
正解:D
順位(1位、2位、3位)には明確な区別があるため、順列を用いる。
7人の中から3人を選んで並べる計算となる。
金メダルの候補は7人。
銀メダルは、金メダル以外の残り6人。
銅メダルは、残りの5人から決まる。
これらを掛け合わせる。
7×6×5=210
よって、210通りである。
ちなみに、順位を区別しない「3人の入賞者」を選ぶだけなら組み合わせ(35通り)となるが、今回は順位があるため注意が必要だ。
問題6(難易度:★★☆☆☆)
問題
以下の問いについて、その組み合わせが何通りあるか答えなさい。
ある会社の新人研修において、6名の新入社員が配属された。この中から、来週開催される外部セミナーに参加する代表者を2名選ぶことになった。選ばれる2名に役割の区別はないものとするとき、選び方は何通りあるか。
選択肢
正解:B
代表者2名にリーダー等の区別はないため、組み合わせ(6C2)で計算する。
計算式は、6×5を2×1で割ることで求められる。
(6×5)÷(2×1)=30÷2=15よって、15通りである。
もし役割(正代表・副代表など)がある場合は順列(6×5=30通り)になるが、今回は単なる「選出」なので2で割ることを忘れてはならない。
問題7(難易度:★★☆☆☆)
問題
以下の問いについて、その組み合わせが何通りあるか答えなさい。
文房具店で、7色の異なるボールペンが販売されている。友人のプレゼント用に、この中から好きな色を3本選んでセットにして購入する場合、色の組み合わせは何通りあるか。
選択肢
正解:B
選ぶ3本の色に順序は関係ないため、組み合わせ(7C3)の計算をおこなう。分子は7から数を下げて3つ掛け合わせ、分母は3×2×1で割る。(7×6×5)÷(3×2×1)=210÷6=35よって、35通りである。順列の計算(7×6×5=210通り)と混同しやすいが、選ばれた3本のセット内容が同じであれば区別しないため、必ず重複分で割る必要がある。
問題8(難易度:★★☆☆☆)
問題
以下の問いについて、条件を満たす選び方が何通りあるか答えなさい。
袋の中に赤玉が6個、白玉が3個入っている。この中から同時に3個の玉を取り出すとき、白玉が少なくとも1個含まれる取り出し方は何通りあるか。
選択肢
正解:D
「少なくとも1個」という条件があるため、余事象を用いる。
この場合の余事象は「3個とも赤玉である」ケースだ。
まず、すべての玉9個(赤6+白3)から3個を選ぶ全体の通り数を求める。
(9×8×7)÷(3×2×1)=84通り
次に、余事象である「赤玉6個から3個を選ぶ」通り数を求める。
(6×5×4)÷(3×2×1)=20通り
最後に全体から余事象を引く。
84-20=64よって、64通りである。
「少なくとも1個」を見たら、反射的に「全体−0個の場合」で考えられるようにしておきましょう。
白が1・2・3個……と分けて数えると、時間もミスも増えます。また、同時に取り出すということは、順番は問わないので、順列ではなく組合せで数えるのが鉄則です。
SPIでは、日本語の条件(同時や順番、代表者など)が、順列か組合せかの判断ポイントになることを意識しましょう。
問題9(難易度:★★☆☆☆)
問題
以下の問いについて、円形のテーブルのまわりに着席する際の座り方は何通りあるか答えなさい。なお、座席の数は全人数と同じであるとする。また、回転して一致する並びは同じものとみなす。
会社の役員会議に、社長、副社長を含む計7人の役員が出席する。このとき、社長と副社長が必ず隣り合うように座るとすると、座り方は何通りあるか。
選択肢
正解:B
社長と副社長の2人を「1つのセット」とみなす。
セット1つと残りの役員5人、計6つの要素を円形に並べる円順列となる。
円順列の公式(要素数-1)の階乗より、(6-1)の階乗=120通り。
さらに、セットにした社長と副社長の並び順(左右)が2通りある。
これらを掛け合わせる。
120×2=240よって、240通りである。
問題10(難易度:★★☆☆☆)
問題
指定された数字カードを使い、条件を満たす整数が何個作れるかを答えなさい。なお、同じカードを2回以上使うことはできないものとする。
0、1、2、3、4の5枚のカードがある。この中から3枚を選んで並べ、3けたの整数を作るとき、整数は全部で何個できるか。
選択肢
正解:C
3けたの整数を作る際、最高位である「百の位」に0は使えない点に注意する。
百の位は、0以外の1~4の中から選ぶため、4通り。
十の位は、残りの4枚(百の位で使った1枚以外、0も使用可能)から選ぶため、4通り。
一の位は、残りの3枚から選ぶため、3通り。
これらを掛け合わせる。
4×4×3=48よって、48個。
単純な順列(5P3=60)と間違えないよう、0の扱いに注意が必要である。
0を含むカードの整数問題での典型的なミスは、「先頭に0は置けない」制約を忘れてしまうことです。
カードの数字だけに目を奪われず、「3けた整数とは何か?」を一度立ち止まって確認しましょう。おすすめは、最初に千の位(先頭)を決めてから残りを並べる型で解くことです。
毎回この順番で考えるようにすると、制約の見落としをかなり防げますよ。
問題11(難易度:★★☆☆☆)
問題
以下の問いについて、条件を満たすパターンや組み合わせが何通りあるか答えなさい。
ある企業の社員IDは、1、2、3、4、5の5種類の数字を使って設定される。この数字を重複して使っても良いとして、3桁の社員IDを作るとき、IDは全部で何通りできるか。
選択肢
正解:D
同じ数字を何度も使って良い「重複順列」の問題である。
3つの位(百の位、十の位、一の位)それぞれについて考える。
百の位は、1〜5の5通りから選べる。
十の位も、同じく5通りから選べる。
一の位も、同じく5通りから選べる。
これらを掛け合わせる。
5×5×5=125よって、125通りである。
異なる数字を選ぶ順列(5×4×3=60)と混同しないよう注意する。
問題12(難易度:★★☆☆☆)
問題
以下の問いについて、条件を満たすパターンや組み合わせが何通りあるか答えなさい。
A、B、C、Dの4人の友人が集まり、一度だけ「じゃんけん」をおこなうことになった。このとき、4人の手の出し方は全部で何通りあるか。
選択肢
正解:C
4人がそれぞれ「グー」「チョキ」「パー」の3種類の手から1つを選ぶ重複順列と考えることができる。
Aさんの手の出し方は3通り。
Bさん、Cさん、Dさんも同様にそれぞれ3通りである。
これらを掛け合わせる。
3×3×3×3=81よって、81通りである。
「4人が3種類を選ぶ」ので3の4乗となるが、「3人が4種類を選ぶ(4の3乗=64)」と逆にしてしまわないよう注意が必要である。
問題13(難易度:★★☆☆☆)
問題
以下の問いについて、条件を満たす結果の出方(組み合わせや並び方)は何通りあるか答えなさい。
ある新人研修で、全5問の○×クイズが出題された。各問題の答えは必ず「○」か「×」のいずれかである。このクイズにおいて、ちょうど3問正解するような正解・不正解のパターンは何通りあるか。
選択肢
正解:A
5問のうち、どの3問で正解するかを選ぶ「組み合わせ」の問題である。
○×という2択の結果が連続するコイントスと同じ構造(反復試行)ととらえることができる。
5問から正解する3問を選ぶため、計算式は5C3となる。
これは正解しない2問を選ぶ5C2と等しい。
(5×4)÷(2×1)=10よって、10通りである。
問題14(難易度:★★☆☆☆)
問題
以下の問いについて、条件を満たす結果の出方(組み合わせや並び方)は何通りあるか答えなさい。
営業担当の田中氏は、1週間のうち月曜日から日曜日までの7日間で、飛び込み営業を毎日おこなった。その結果、成約できた日がちょうど2日あった場合、成約した曜日の組み合わせは何通り考えられるか。
選択肢
正解:B
7日間のうち、成約となる2日を選ぶ組み合わせの問題である。
順序は関係なく、単に「どの曜日か」を選ぶため、組み合わせの公式(7C2)を用いる。
分子は7×6、分母は2×1となる。
(7×6)÷(2×1)=42÷2=21
よって、21通りである。
順列(7P2=42通り)と間違えないよう注意が必要である。
問題15(難易度:★★☆☆☆)
問題
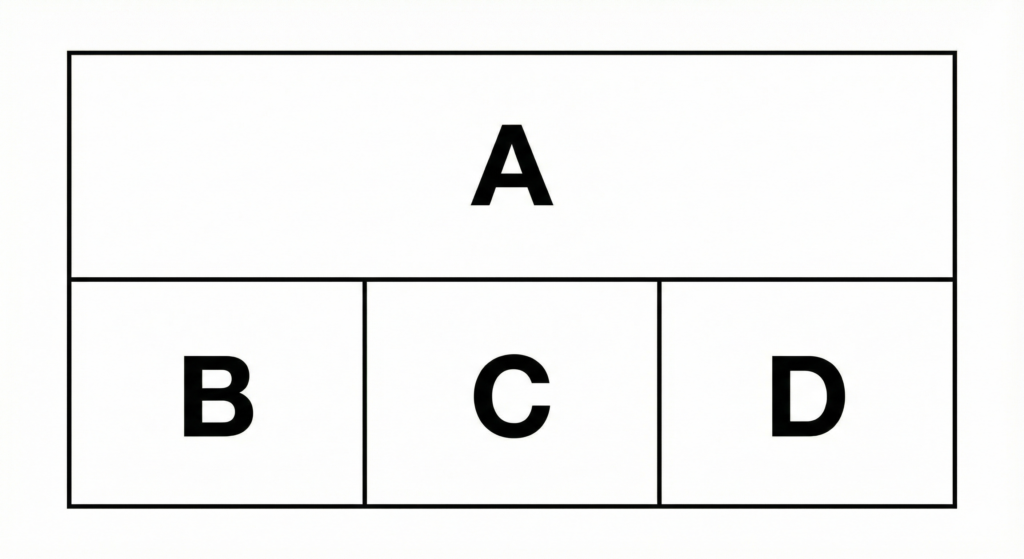
画像のように、長方形が4つの領域(上部のA、下部左のB、下部中央のC、下部右のD)に区分けされている。これらの領域を指定された色を使って塗り分ける。ただし、隣り合う領域には異なる色を使わなければならない。
この4つの領域を、赤・青・緑・黄の4色のいずれかを用いて塗り分ける。ただし、「領域Aは必ず赤色」で塗らなければならない。この場合、塗り方は全部で何通りあるか。なお、同じ色を何度も使って良いものとする。
選択肢
正解:B
特定の色が固定されている条件付きの問題である。
Aの色:赤色で固定(1通り)。
Cの色:A(赤)以外から選ぶため、残り3色から選ぶ(3通り)。
Bの色:A(赤)とC(選んだ1色)以外から選ぶ。残りの2色から選ぶ(2通り)。
Dの色:A(赤)とC(選んだ1色)以外から選ぶ。残りの2色から選ぶ(2通り)。
これらを掛け合わせる。1×3×2×2=12よって、12通りである。
問題16(難易度:★★★☆☆)
問題
以下の問いについて、その組み合わせや並び方が何通りあるか答えなさい。
新規プロジェクトの立ち上げにともない、優秀な社員8名が候補に挙がった。この中から、プロジェクトを統括する「責任者」、現場を指揮する「リーダー」、技術をサポートする「技術顧問」をそれぞれ1名ずつ任命したい。3名の役割分担の決め方は全部で何通りあるか。
選択肢
正解:C
3つのポスト(責任者・リーダー・技術顧問)はそれぞれ役割が異なるため、順列で計算する。
8名から3名を選んで配置する。
責任者の選び方は8通り。
リーダーの選び方は、残りの7通り。
技術顧問の選び方は、さらに残りの6通り。
計算式は以下のようになる。
8×7×6=336
よって、336通りである。
単に3人を選ぶだけの56通り(8C3)と混同しないよう注意が必要である。
問題17(難易度:★★★☆☆)
問題
以下の問いについて、その組み合わせが何通りあるか答えなさい。
社内コンペのために、開発部のメンバー8人の中からプロジェクトチームを結成することになった。ここから3人のメンバーを選出する場合、そのメンバー構成は何通り考えられるか。
選択肢
正解:B
メンバー3人の役割に区別はないため、組み合わせ(8C3)を用いる。
分子は8×7×6、分母は3×2×1となる。
(8×7×6)÷(3×2×1)=336÷6=56よって、56通りである。
計算時、分母の「3×2×1」と分子の「6」を先に約分してしまうと、8×7=56となり、素早く計算できる。
順列の336通りを選ばないよう注意が必要だ。
問題18(難易度:★★★☆☆)
問題
以下の問いについて、条件を満たす選び方が何通りあるか答えなさい。
ある工場で製造された製品が10個あり、そのうち7個が良品、3個が不良品であることがわかっている。品質検査のためにこの中から無作為に3個を選び出すとき、不良品が少なくとも1個含まれる選び方は何通りあるか。
選択肢
正解:C
「不良品が少なくとも1個」の余事象は「選んだ3個すべてが良品」となる場合である。
全体の選び方は、10個から3個を選ぶ組み合わせ。
(10×9×8)÷(3×2×1)=120通り
余事象の選び方は、良品7個から3個を選ぶ組み合わせ。
(7×6×5)÷(3×2×1)=35通り
全体から余事象を引いて答えを出す。
120-35=85
よって、85通りである。
問題19(難易度:★★★☆☆)
問題
以下の問いについて、円形のテーブルのまわりに着席する際の座り方は何通りあるか答えなさい。なお、座席の数は全人数と同じであるとする。また、回転して一致する並びは同じものとみなす。
仲の良い学生6人のグループが円卓で食事をすることになった。このうち、特定の3人(A、B、C)が固まって隣り合うように座る場合、その座り方は何通りあるか。
選択肢
正解:C
A、B、Cの3人を「1つのセット」とみなす。
セット1つと残りの3人、計4つの要素を円形に並べる円順列を計算する。
(4-1)の階乗=3×2×1=6通り。
次に、セットにした3人の中での並び順を考える。
3人の順列なので、3×2×1=6通り。
これらを掛け合わせる。
6×6=36よって、36通りである。
セット内の並びが「2通り」ではなく「6通り」になる点に注意が必要だ。
問題20(難易度:★★★☆☆)
問題
以下の問いについて、円形のテーブルのまわりに着席する際の座り方は何通りあるか答えなさい。なお、座席の数は全人数と同じであるとする。また、回転して一致する並びは同じものとみなす。
男性4人、女性3人の計7人が円卓を囲むことになった。このとき、特定の男性2人のペアと、特定の女性2人のペアが、それぞれ隣り合って座る場合、座り方は何通りあるか。
選択肢
正解:C
「男性ペア(X)」と「女性ペア(Y)」をそれぞれセットとみなす。
X、Y、残りの3人(計5つの要素)の円順列を計算する。
(5-1)の階乗=24通り。
次に、それぞれのペア内での並び替えを考える。
男性ペアの並びが2通り、女性ペアの並びが2通り。
すべてを掛け合わせる。
24×2×2=96よって、96通りである。
問題21(難易度:★★★☆☆)
問題
指定された数字カードを使い、条件を満たす整数が何個作れるかを答えなさい。なお、同じカードを2回以上使うことはできないものとする。
0、1、2、3、4、5の6枚のカードがある。この中から4枚を選んで並べ、4けたの「偶数」を作るとき、整数は全部で何個できるか。
選択肢
正解:C
偶数を作るには、一の位が偶数(0、2、4)である必要がある。
0を含む場合、場合分けをして考える。
(1)一の位が「0」の場合千、百、十の位は残りの5枚から3枚選んで並べる。
5×4×3=60通り
(2)一の位が「2」または「4」の場合(2通り)千の位は0と一の位の数を使えないため、4通り。
百、十の位は残りの4枚から2枚選んで並べる
(4×3)。2×4×4×3=96通り
(1)と(2)を足し合わせる。
60+96=156
よって、156個である。
条件が多い問題は、一気に問題を解こうとするほどミスが増えます。
この問題では、①末尾が偶数であること、②先頭は0以外、③4枚を選んで並べる、という3つの条件がありますね。
問題文を読みながら何を考える必要があるかを意識することが大切です。今回の場合は、末尾を固定→残りを順列、という解き方を自分の中のテンプレにしておくと、本番でも安定して解けますよ。
問題22(難易度:★★★☆☆)
問題
指定された数字カードを使い、条件を満たす整数が何個作れるかを答えなさい。なお、同じカードを2回以上使うことはできないものとする。
0、1、2、3、4、5の6枚のカードがある。この中から3枚を選んで並べ、3けたの「5の倍数」を作るとき、整数は全部で何個できるか。
選択肢
正解:C
5の倍数となる条件は、一の位が「0」または「5」であること。
これも0の有無で場合分けをおこなう。
(1)一の位が「0」の場合百、十の位は残りの5枚から2枚選んで並べる。
5×4=20通り
(2)一の位が「5」の場合百の位は0と5を使えないため、4通り。
十の位は残り(0復活)の4通り。
4×4=16通りこれらを足し合わせる。
20+16=36
よって、36個である。
一の位が5の時、百の位に0が置けないことを忘れると誤答(40個)になる。
問題23(難易度:★★★☆☆)
問題
指定された数字を使い、条件を満たす整数が何個作れるかを答えなさい。
「0、1、2、3」の4種類の数字を使って3桁の整数を作る。同じ数字を何度使っても良いとき、作ることができる整数は何個あるか。
選択肢
正解:C
3桁の整数を作る場合、最高位である百の位に「0」を使うことはできない。
百の位は、1、2、3の3通り。
十の位は、0を含めた4通りすべて使える。
一の位も、0を含めた4通りすべて使える。
これらを掛け合わせる。
3×4×4=48
よって、48個である。
単純な4の3乗(64通り)から、百の位が0になる不適格なケースを除外するという視点が必要だ。
問題24(難易度:★★★☆☆)
問題
以下の問いについて、条件を満たす結果の出方(組み合わせや並び方)は何通りあるか答えなさい。
工場で製造された製品の品質チェックをおこなっている。製品をランダムに1個ずつ取り出して検査する、という作業を8回おこなったところ、そのうち5回は「良品」、3回は「不良品」という判定結果になった。この結果を1回から8回まで順に並べたとき、想定される良品・不良品の判定の並び方は何通りあるか。
選択肢
正解:B
8回の検査結果のうち、どの5回で良品が出たかを選ぶ計算(8C5)となる。
8個から5個選ぶ計算は、残りの3個(不良品)を選ぶ計算(8C3)と同じ結果になるため、計算が楽な8C3で求める。
(8×7×6)÷(3×2×1)=336÷6=56
よって、56通りである。
問題25(難易度:★★★☆☆)
問題
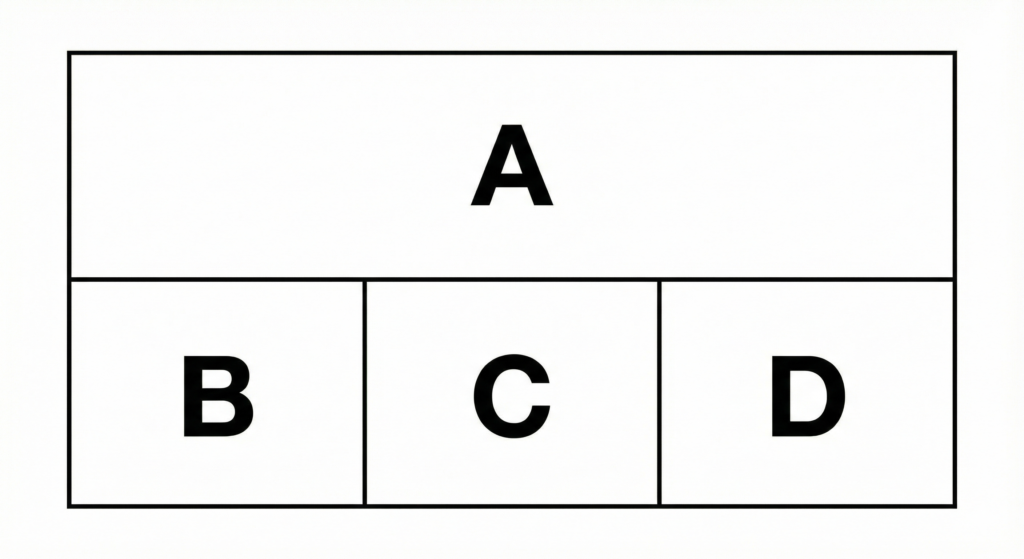
画像のように、長方形が4つの領域(上部のA、下部左のB、下部中央のC、下部右のD)に区分けされている。これらの領域を指定された色を使って塗り分ける。ただし、隣り合う領域には異なる色を使わなければならない。
この4つの領域を、赤・青・緑・黄の4色のいずれかを用いて塗り分ける。このとき、離れている「領域Bと領域Dが同じ色」になるような塗り方は何通りあるか。
選択肢
正解:B
離れている箇所(BとD)を同色にする拘束条件がある場合、そこをセットにして考えると計算がスムーズです。
1.Aの色:4色から自由に選べる(4通り)。
2.Bの色:Aと隣り合っているため、A以外の3色から選ぶ(3通り)。
3.Dの色:「Bと同じ色にする」という条件があるため、Bの色が決まれば自動的に1通りに決まる(1通り)。
4.Cの色:AおよびB(=D)と隣り合っている。AとBはすでに異なる色になっているため、残りの2色から選ぶ(2通り)。
これらを掛け合わせます。
4×3×1×2=24
よって、24通りである。
問題26(難易度:★★★★☆)
問題
以下の問いについて、条件を満たす選び方が何通りあるか答えなさい。
ある地域のボランティア活動に、経験者が4人、未経験者が6人の計10人が応募した。この中から活動メンバーとして4人を選出するとき、経験者が少なくとも1人含まれる選び方は何通りあるか。
選択肢
正解:B
選ぶ人数が4人に増えているが、考え方は同じく余事象を使う。
「経験者が少なくとも1人」の反対は「全員が未経験者」である。
全体は10人から4人を選ぶ。
(10×9×8×7)÷(4×3×2×1)=210通り
余事象は未経験者6人から4人を選ぶ。
これは6人から選ばない2人を選ぶのと同じ計算になる。
(6×5)÷(2×1)=15通り全体から引く。
210-15=195よって、195通りである。
問題27(難易度:★★★★☆)
問題
以下の問いについて、円形のテーブルのまわりに着席する際の座り方は何通りあるか答えなさい。なお、座席の数は全人数と同じであるとする。また、回転して一致する並びは同じものとみなす。
ある委員会のメンバーとして、A氏とB氏を含む7人が円卓に着席する。A氏とB氏は意見が対立しているため、決して隣り合わないように座らせたい。このときの座り方は何通りあるか。
選択肢
正解:C
「隣り合わない」場合は、全体の順列から「隣り合う」ケース(余事象)を引くのが効率的だ。
まず、7人全員を円形に並べる全通り数は、(7-1)の階乗=720通り。
次に、A氏とB氏が隣り合うケースを計算する。
(6-1)の階乗×2=240通り。
最後に引き算をおこなう。
720-240=480
よって、480通りである。
問題28(難易度:★★★★☆)
問題
指定された数字カードを使い、条件を満たす整数が何個作れるかを答えなさい。なお、同じカードを2回以上使うことはできないものとする。
0、1、2、3、4、5の6枚のカードがある。この中から4枚を選んで並べ、4けたの整数を作るとき、「4200より大きい」整数は何個できるか。
選択肢
正解:C
千の位の数字によって場合分けをおこなう。
(1)千の位が「5」の場合4200より必ず大きくなる。
残りの3けたは5枚から3枚選ぶ順列。
5×4×3=60通り
(2)千の位が「4」の場合百の位が2以上(2、3、5)であれば4200より大きくなる(0、1は不可)。
百の位は3通り。
十、一の位は残りの4枚から2枚選ぶ。
3×4×3=36通り
これらを足し合わせる。
60+36=96
よって、96個である。
問題29(難易度:★★★★☆)
問題
以下の問いについて、条件を満たすパターンや組み合わせが何通りあるか答えなさい。
花壇にある一列に並んだ3つの区画に、パンジー、チューリップ、マリーゴールド、ヒマワリの4種類の花を植えることになった。1つの区画には1種類の花だけを植え、隣り合う区画には異なる種類の花を植えるとき、植え方は何通りあるか。なお、同じ種類の花を(隣り合わなければ)何度使っても良いものとする。
選択肢
正解:B
左端の区画から順に考えていく。
1つ目の区画は、4種類どの花でも良いので4通り。
2つ目の区画は、1つ目で選んだ花以外であれば良いので3通り。
3つ目の区画は、2つ目で選んだ花以外であれば良いので(1つ目と同じ花でも可)3通り。
これらを掛け合わせる。
4×3×3=36よって、36通りである。
順列や単純な重複順列とは異なる、「直前の選択肢を除く」という考え方がポイントである。
問題30(難易度:★★★★☆)
問題
以下の問いについて、条件を満たす結果の出方(組み合わせや並び方)は何通りあるか答えなさい。
AチームとBチームが野球の試合を5回おこなった。引き分けはないものとするとき、AチームがBチームに「勝ち越す(勝ち数が負け数より多い)」勝敗のパターンは全部で何通りあるか。
選択肢
正解:C
5試合で勝ち越すケースは、「3勝2敗」「4勝1敗」「5勝0敗」の3つのパターンがある。
これらを個別に計算して足し合わせる。
(1)3勝の場合:5C3=10通り
(2)4勝の場合:5C4=5通り
(3)5勝の場合:5C5=1通り
これらを合計する。
10+5+1=16
よって、16通りである。
全体の半数が勝ち越しになる(全32通りの半分=16通り)という対称性に気づくと即答も可能。
問題31(難易度:★★★★☆)
問題
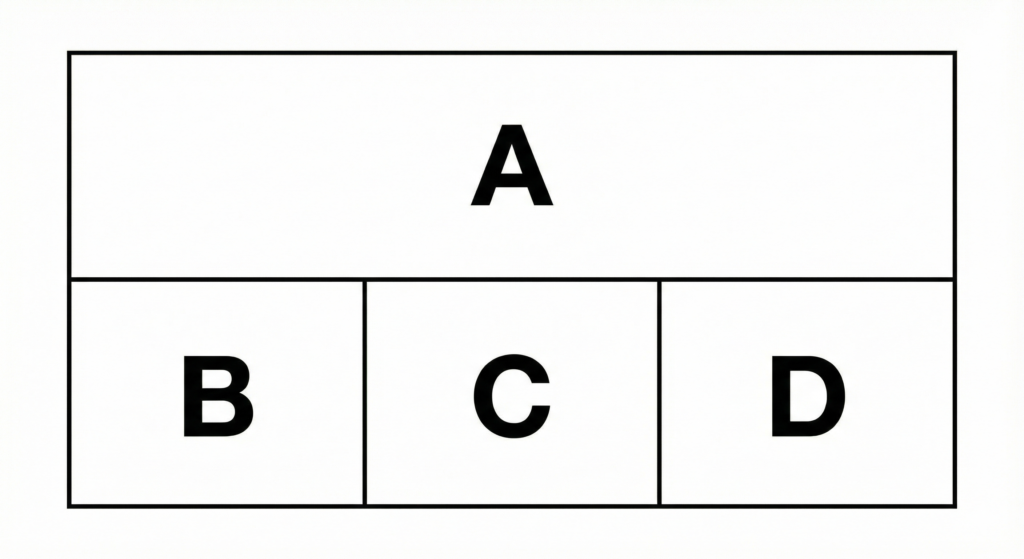
画像のように、長方形が4つの領域(上部のA、下部左のB、下部中央のC、下部右のD)に区分けされている。これらの領域を指定された色を使って塗り分ける。ただし、隣り合う領域には異なる色を使わなければならない。
この4つの領域を、赤・青・緑・黄の4色を用いて塗り分ける。このとき、離れている「領域Bと領域Dが異なる色」になるような塗り方は何通りあるか。
選択肢
正解:B
BとDが異なる色の場合、4つの領域すべてに異なる色(4色すべて)を使って塗り分けることになる。
1.Aの色:4色から自由に選べる(4通り)。
2.Cの色:Aと隣り合うため、A以外の3色から選ぶ(3通り)。
3.Bの色:AおよびCと隣り合っており、かつAとCは色が異なるため、残りの2色から選ぶ(2通り)。
4.Dの色:A、Cと隣り合い、さらに条件によりBとも異なる色にする必要があるため、残りの1色に決まる(1通り)。
これらを掛け合わせる。
4×3×2×1=24
よって、24通りである。
問題32(難易度:★★★★★)
問題
以下の問いについて、条件を満たす選び方が何通りあるか答えなさい。
男性6人、女性4人の計10人のグループがある。この中から委員を4人選ぶとき、女性が「少なくとも2人」含まれる選び方は何通りあるか。
選択肢
正解:B
「少なくとも2人」の場合、条件を満たさない余事象は「女性が0人」または「女性が1人」の2つのケースとなる。
全体は10人から4人を選ぶので210通り。
余事象①(女性0人=全員男性):男性6人から4人選ぶので15通り。
余事象②(女性1人):女性4人から1人、男性6人から3人選ぶ。
(4÷1)×{(6×5×4)÷(3×2×1)}=80通り。
これらを全体から引く。
210-(15+80)=210-95=115
よって、115通りである。
「少なくとも2人」という表現は、多くの学生が場合分けで混乱しやすいポイントです。
女性2・3・4人の場合をすべて足し合わせるゴリ押しも方法としてありですが、「全体−(女性0人+女性1人)」と補集合で処理するクセをつけるのがおすすめです。
その際、男女を分けて人数を決め、男性の選び方×女性の選び方の形で整理すると、計算の見通しが一気に良くなります。
問題33(難易度:★★★★★)
問題
以下の問いについて、条件を満たすパターンや組み合わせが何通りあるか答えなさい。
ある定食屋には「A定食」「B定食」「C定食」の3種類のメニューがある。ある客が月曜日から金曜日までの5日間、毎日これらの中から1つ選んで昼食をとるとき、「A定食」を少なくとも1回は選ぶパターンは何通りあるか。
選択肢
正解:C
「少なくとも1回」という条件があるため、全体のパターン数から「A定食を1回も選ばない(すべてBかC)」パターン(余事象)を引いて求める。
全体のパターンは、3種類から5回選ぶので、3の5乗=243通り。
A定食を選ばないパターンは、BかCの2種類から5回選ぶので、2の5乗=32通り。
全体から余事象を引く。
243-32=211よって、211通りである。
問題34(難易度:★★★★★)
問題
以下の問いについて、条件を満たす結果の出方(組み合わせや並び方)は何通りあるか答えなさい。
あるロボットが直線上を移動する実験をおこなう。1回の指令につき、「右へ1m」または「左へ1m」のどちらか一方に必ず動く。この指令を計10回出した結果、スタート地点から見て「右へちょうど2m」の位置にロボットがいた。このときの移動プロセスのパターンは何通り考えられるか。
選択肢
正解:D
まず、右に移動した回数と左に移動した回数を特定する。
右への移動をx回、左への移動をy回とすると、合計10回なのでx+y=10。
右を正(+)、左を負(ー)とすると、最終的な位置が+2なのでx-y=2。
この連立方程式を解くと、x=6、y=4となる。
つまり、10回の移動のうち、右への移動が6回(左が4回)選ばれる組み合わせを求めればよい。
計算は10C6(=10C4)となる。
(10×9×8×7)÷(4×3×2×1)=210よって、210通りである。
このタイプは「ランダムに動く=数えきれない」と感じてしまいがちですが、落ち着いて条件を式にすることが最重要です。
右を+1、左を−1とみなし、合計10回や最終的に+2という情報を連立方程式に落としてから、組合せで位置を数えます。
すぐにC(10,5)などと書かず、「何回右で何回左か」を確定させてから数えるのがコツです。確率・場合の数の応用問題にもつながる考え方なので、プロセスごと身に付けましょう。
問題35(難易度:★★★★★)

問題
画像のように、長方形が4つの領域(上部のA、下部左のB、下部中央のC、下部右のD)に区分けされている。これらの領域を指定された色を使って塗り分ける。ただし、隣り合う領域には異なる色を使わなければならない。
この4つの領域を、赤・青・緑・黄の4色のいずれかを用いて塗り分ける。このとき、「赤色は必ず1カ所だけ」に使われるような塗り方は何通りあるか。
選択肢
正解:D
赤色を使う場所で場合分けをして、それぞれのパターンを足し合わせる。赤色以外の場所は、残り3色(青・緑・黄)で塗り分ける。
1.Aが赤の場合:
B・C・Dを残り3色で塗る。Aはすでに赤のため、B・C・Dがそれぞれ隣り合う色と重複しないように選ぶ。Cは残り3通り、BはC以外で2通り、DはC以外で2通りとなる。(1×3×2×2=12通り)
2.Cが赤の場合:
A・B・Dを残り3色で塗ります。Aは残り3通り、BはAとC(赤)以外で2通り、DはAとC(赤)以外で2通りとなる。(1×3×2×2=12通り)
3.Bが赤の場合:
Aは赤不可(残り3通り)、Cは赤とA以外(残り2通り)、Dは赤とAとC以外(残り1通り)となる。(1×3×2×1=6通り)
4.Dが赤の場合:
Bの場合と同様に、対称性から6通りとなる。
合計:12+12+6+6=36
よって、36通りである。
練習問題が解けたら、次はSPI模試に挑戦して実力をチェックしてみましょう。
SPI「場合の数」を対策する際のポイント
SPIの非言語に関する記事
◇非言語の対策
SPI非言語は対策すれば怖くない! 出題傾向や例題を徹底解説
SPIに関する記事
◇解答時間
SPIの解答時間を受検方式別に解説! 時間切れを防ぐコツ10選も
◇勉強法
効率抜群なSPIの勉強法|出題形式と頻出問題を踏まえた対策を伝授
◇勉強時間
SPIの勉強時間をプロが解説! おすすめの進め方や重点ポイントも
場合の数以外の練習問題も解いてみよう!
SPIは多くの分野に分かれています。練習問題を繰り返し解いて、苦手を攻略しましょう。
SPIのそのほかの練習問題
各分野の問題が解けたら、最後にSPI模試に挑戦してみましょう。
執筆・編集 PORTキャリア編集部
> コンテンツポリシー
記事の編集責任者 熊野 公俊 Kumano Masatoshi













アドバイザーからワンポイントアドバイス
国家資格キャリアコンサルタント
小寺 一綺
プロフィールを見るいきなり計算に入らず問題の型を確認する癖をつけよう!
場合の数で最重要なのは、数え方を暗記するのではなく、どう整理すれば数えやすくなるかという考え方の型を身に付けることです。まずは、「1.順番を区別するかどうか」「2.同じものを何度も使って良いか」「3.条件が少なくとも◯か」「4.先頭に置けない数字や0が絡むか」という4つを区別しましょう。
学生の傾向からすると、多くの失点は計算そのものよりも順列か組合せかの選択ミスや場合分けの漏れ、0の扱い忘れから生じます。問題文を読んだらいきなり計算に入らず、4つの区分を数秒でチェックする習慣をつけてください。
「場合の数」の習得におすすめの練習方法
練習の仕方として、まずは★2レベルまでの典型問題(人数・席順・カード・玉など)で、パターンごとの型を確認します。
そのうえで、条件付きの問題(少なくともや隣り合う/隣り合わない、末尾が◯◯など)を集中的に演習し、補集合で一気に数えたり、かたまりに置き換えたりといったテクニックを反復しましょう。
1日20〜30分でも良いので、必ず手を動かして式を書き、1問ごとに「これはなぜ順列なのか」などを自分の言葉で説明してみると、短時間での理解につながりますよ!