- ファイナンシャルフィールド（コラム掲載）
- ハピママ（マネー系コラム掲載）
SPIの「グラフの領域」は、提示された不等式が示す範囲から条件に合致する領域を選ぶ問題です。基本的にはペーパーテストでのみ出題される単元ですが、出題傾向が変わる可能性もあるのでそのほかの形式で受験する人も対策しておくと良いでしょう。
この記事では、非言語領域を得意とする山田さんとともにSPIの「グラフの領域」の解き方について解説していきます。頻出のグラフについても詳しく解説しているので、不等式の理解を深める手助けにしてください。
記事の後半には「グラフの領域」の練習問題を6問用意しています。直線を用いた基礎的なものから、円を用いた応用問題まで網羅的に紹介しているのでぜひ腕試しに解いてみましょう。
よりSPIの本番をイメージして対策したい人は、SPI対策模試にも挑戦してみてください。
SPI「グラフの領域」の概要
- 問題パターン：直線で囲まれた領域、放物線と直線で囲まれた領域、円と直線で囲まれた領域
- 1問当たりの時間：1分～1分半程度
- 出題頻度：テストセンター（出題無し）ペーパーテスト（高）Webテスティング（出題無し）
- グラフの領域を解くときのコツをわかりやすく教えてください！
数式とグラフの形をセットで覚えておくのが大切！
「グラフの領域」については、中学から高校1年生で習う程度の数式と、その数式が描くグラフの形をマスターできているかが重要です。義務教育レベルの数学が不得意であった場合は、やや苦労する出題範囲かもしれません。
とはいえ、出てくるグラフの形はほとんど同じです。
①軸と平行な直線（定数）
②軸に対して斜めの直線（1次関数）
③軸に対しての放物線（2次関数）
④円（2次関数の応用）
上記の4つを覚えておけば十分でしょう。
これらの頻出のグラフについては次の見出しで詳しく解説しているので、不安がある人はしっかり確認しておいてください。
グラフの領域で出題されるグラフの種類
グラフの領域の問題を解くためには、提示された式が「どんな形のグラフになるのか」を理解しておかなければなりません。
ここではSPIで頻出のパターンを紹介するので、式とグラフの形を必ずセットで覚えるようにしましょう。
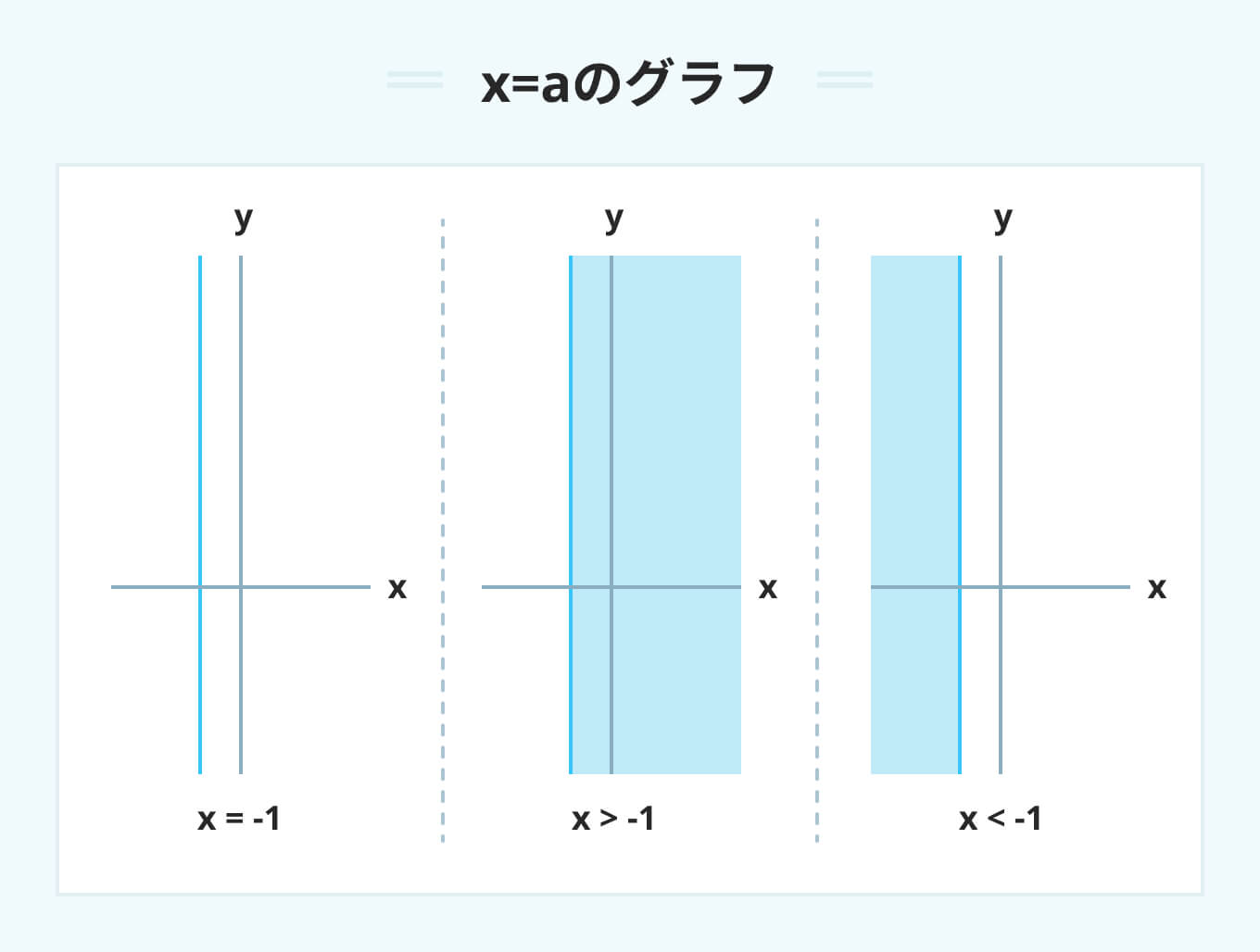
x=aのグラフ
x=aのグラフはy軸と常に平行な直線になります。
x>aの場合はグラフの右側が、x<aの場合はグラフの左側が指し示す領域です。
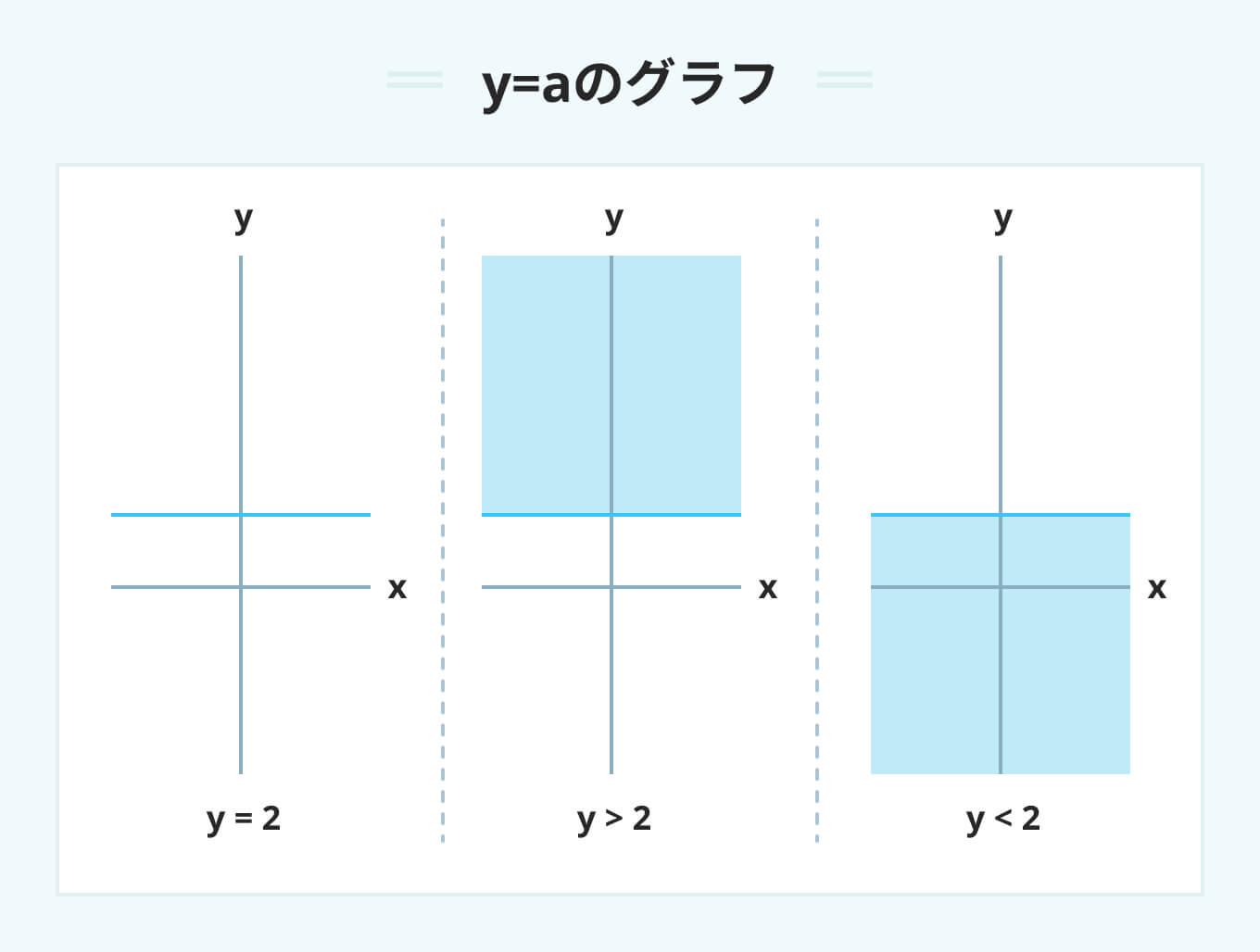
y=aのグラフ
y=aのグラフはx軸と常に平行な直線になります。
y>aの場合はグラフの上側が、y<aの場合はグラフの下側が指し示す領域です。
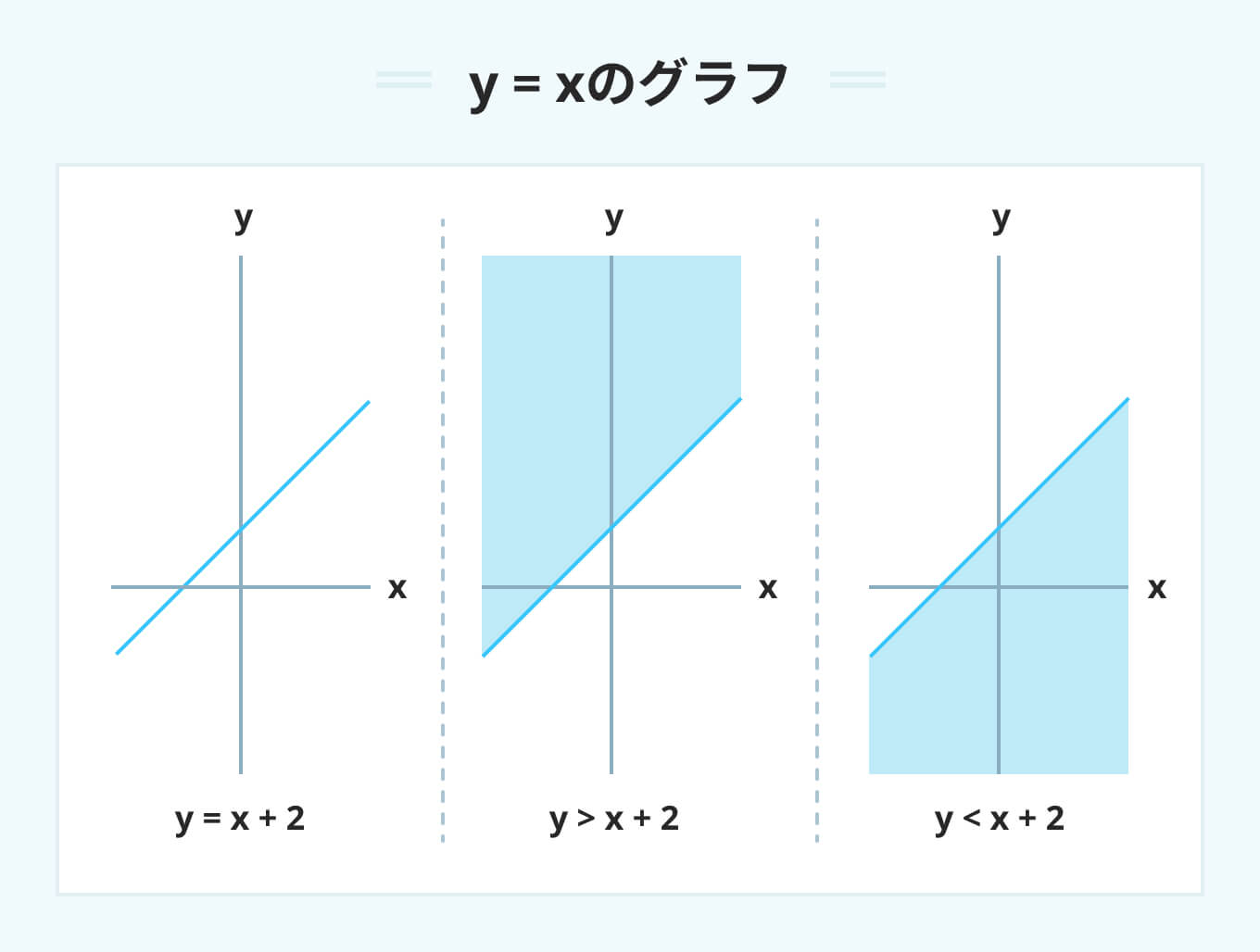
y=xのグラフ
y＝xのグラフは下記の図のような傾いた直線になります。
y>xの場合は直線の上側が、y<xの場合は直線の下側が指し示す領域です。
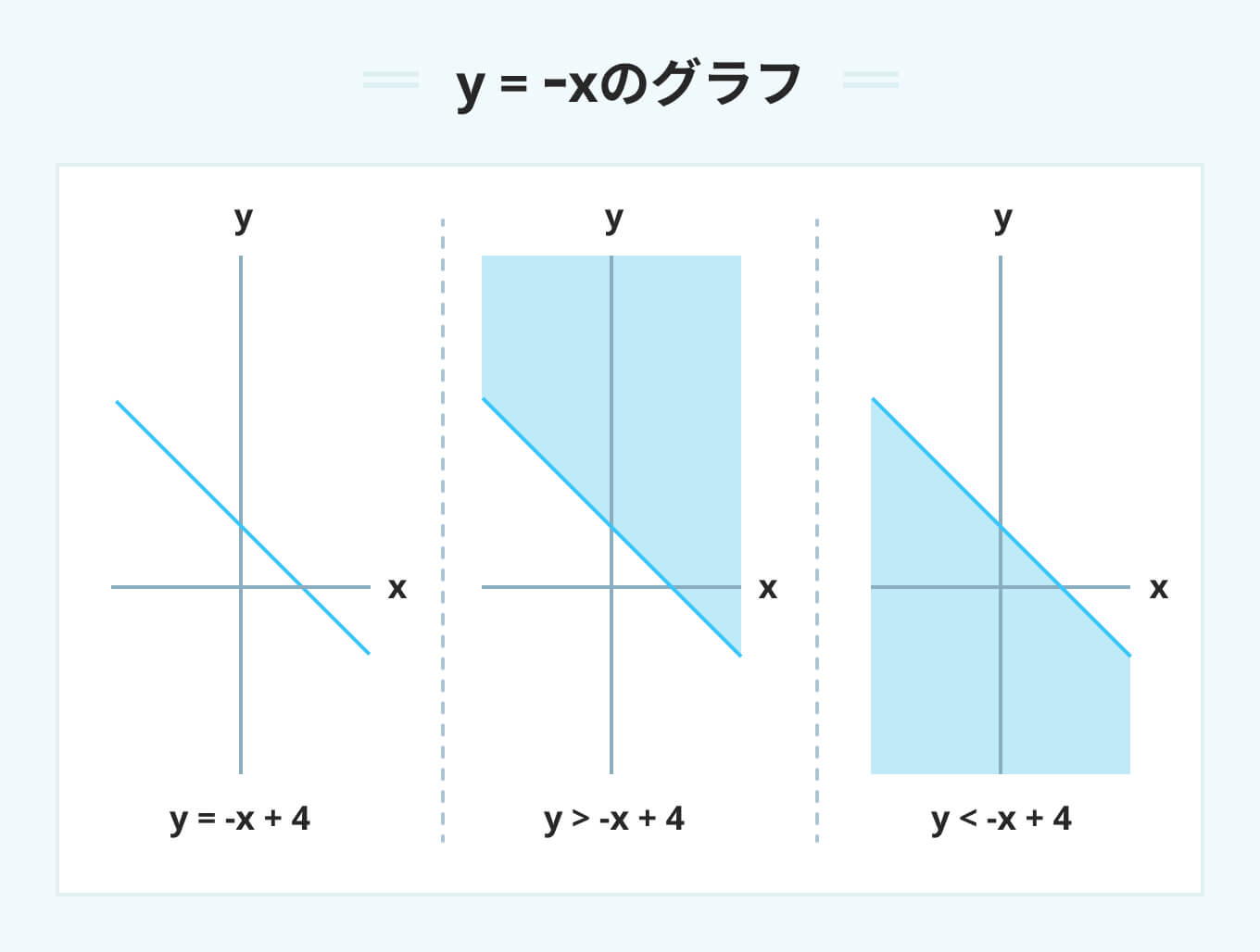
y=-xのグラフ
y=-xのグラフは下記の図のような傾いた直線になります。
y>-xの場合は直線の上側が、y<-xの場合は直線の下側が指し示す領域です。
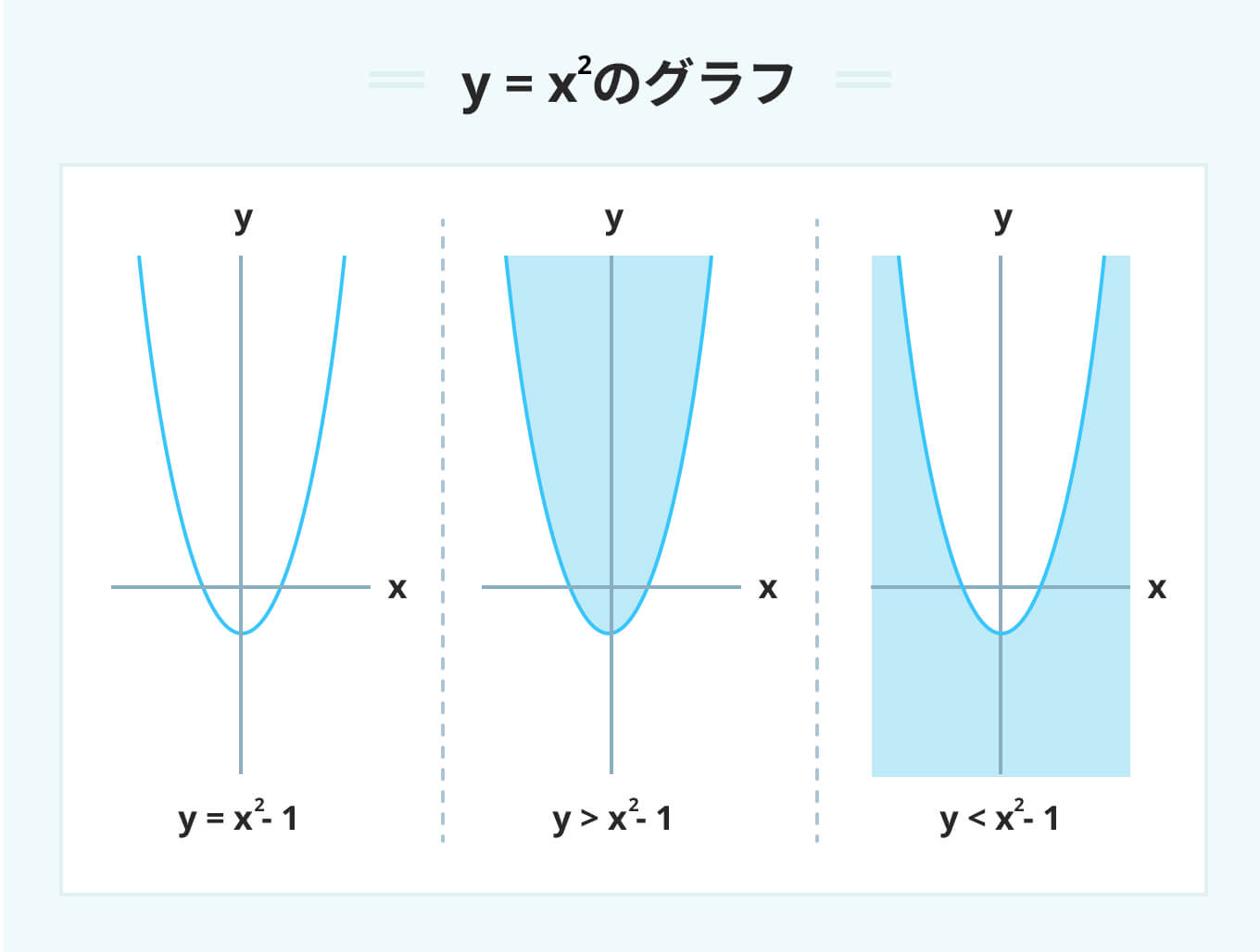
y=x^2のグラフ
y=x^2のグラフは必ず下側に凸の放物線状になります。
y>x^2の場合は放物線の上側が、y<x^2の場合は放物線の下側が指し示す領域です。
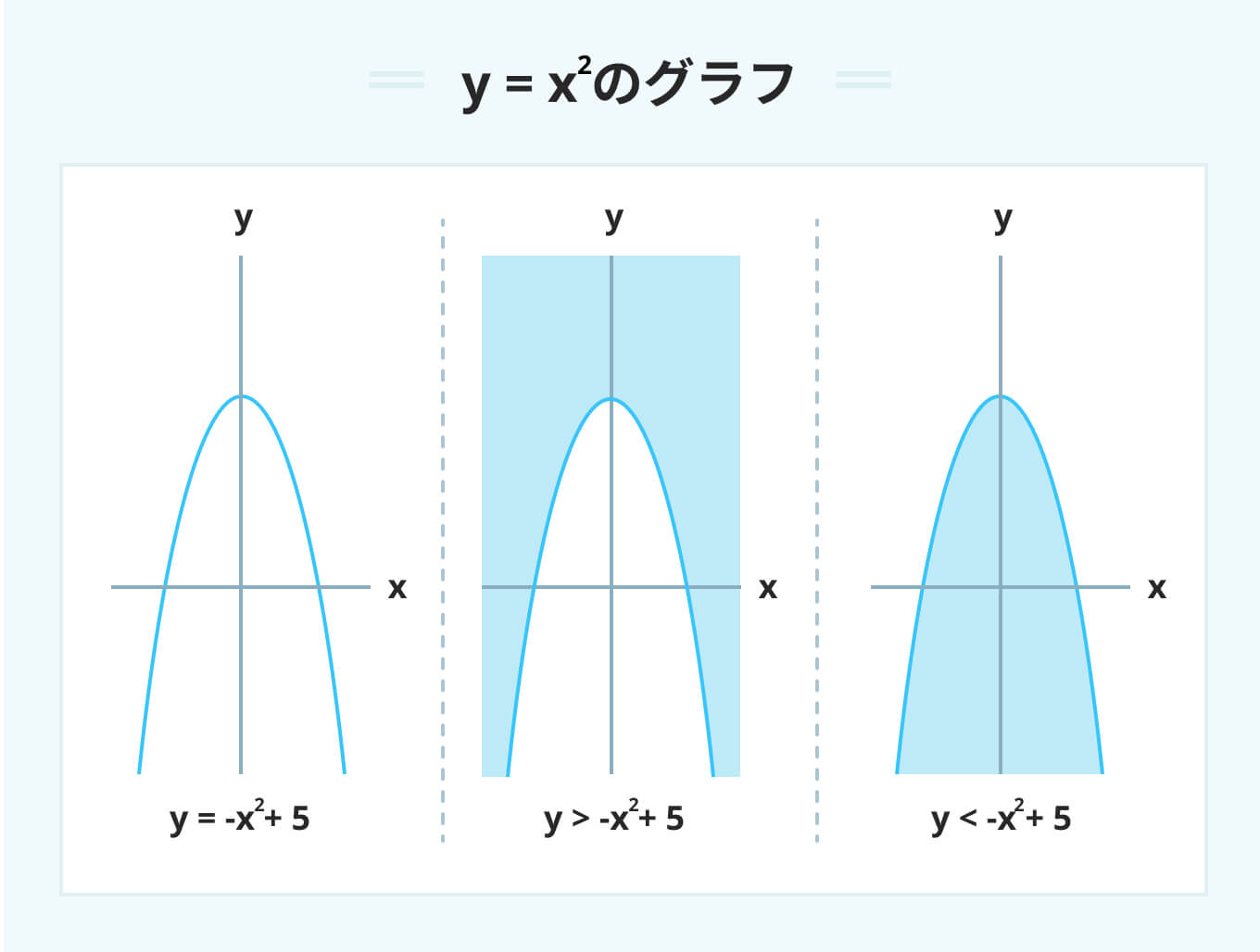
y=-x^2のグラフ
y=-x^2のグラフは必ず上側に凸の放物線状になります。
y>-x^2の場合は放物線の上側が、y<-x^2の場合は放物線の下側が指し示す領域です。
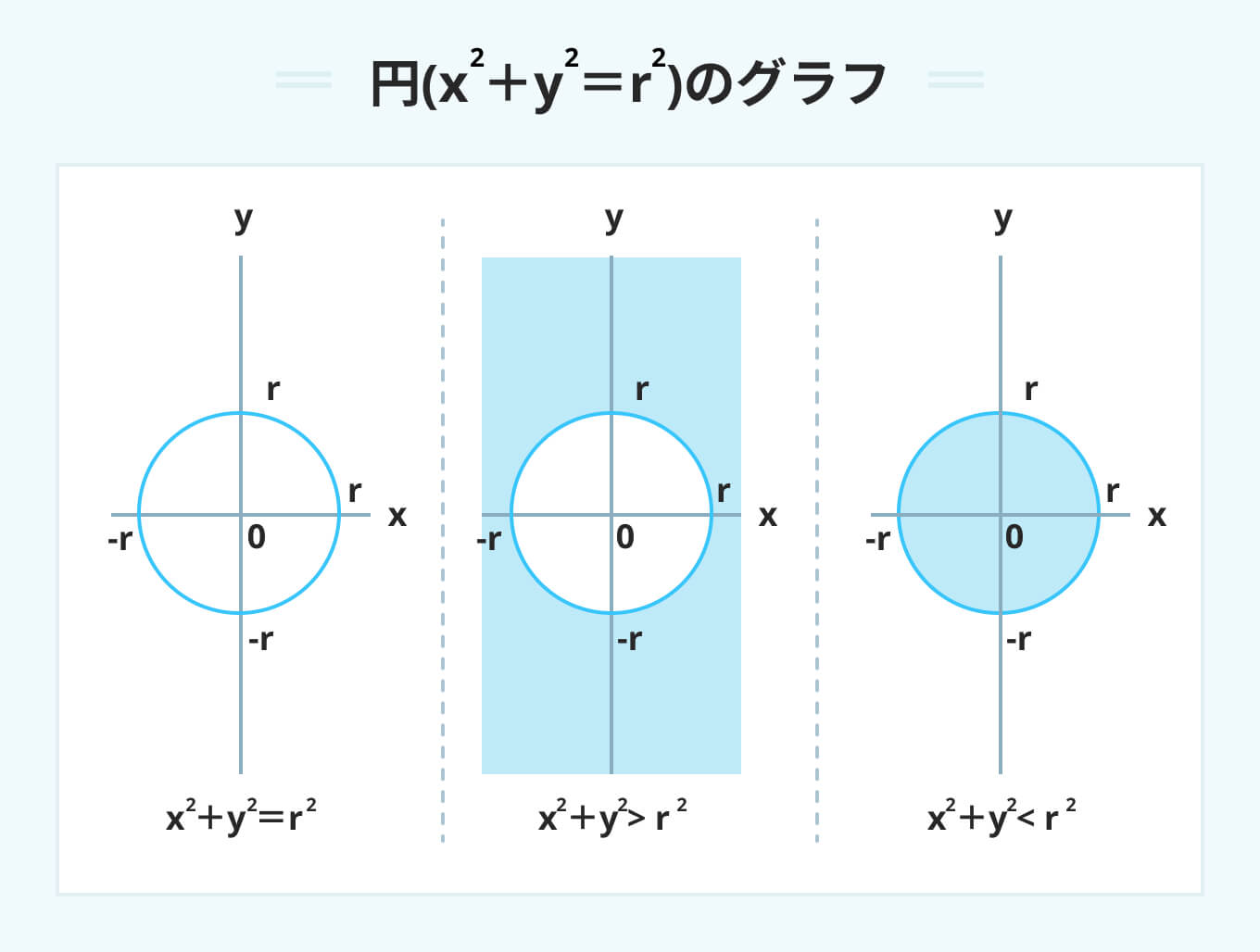
円(x^2＋y^2＝r^2)のグラフ
x^2＋y^2＝r^2は半径rの円を示すグラフになります。
x^2＋y^2>r^2の場合は円の外側が、x^2＋y^2<r^2の場合は円の内側が指し示す領域です。
SPI「グラフの領域」練習問題6問｜山田さんによる解き方の解説付き！
ここからは、SPI「グラフの領域」の練習問題を山田さんの解説付きで6問紹介します。難解な単元だからこそ、しっかりと演習を積んでライバルに差をつけましょう。
初めて取り組む人はいきなり解くとつまずいてしまう恐れがあるので、まず「問題を解く前に確認！ グラフの領域の解答のコツ」を読んでから演習に入るようにしてください。
問題1（難易度：★★☆☆☆）
問題
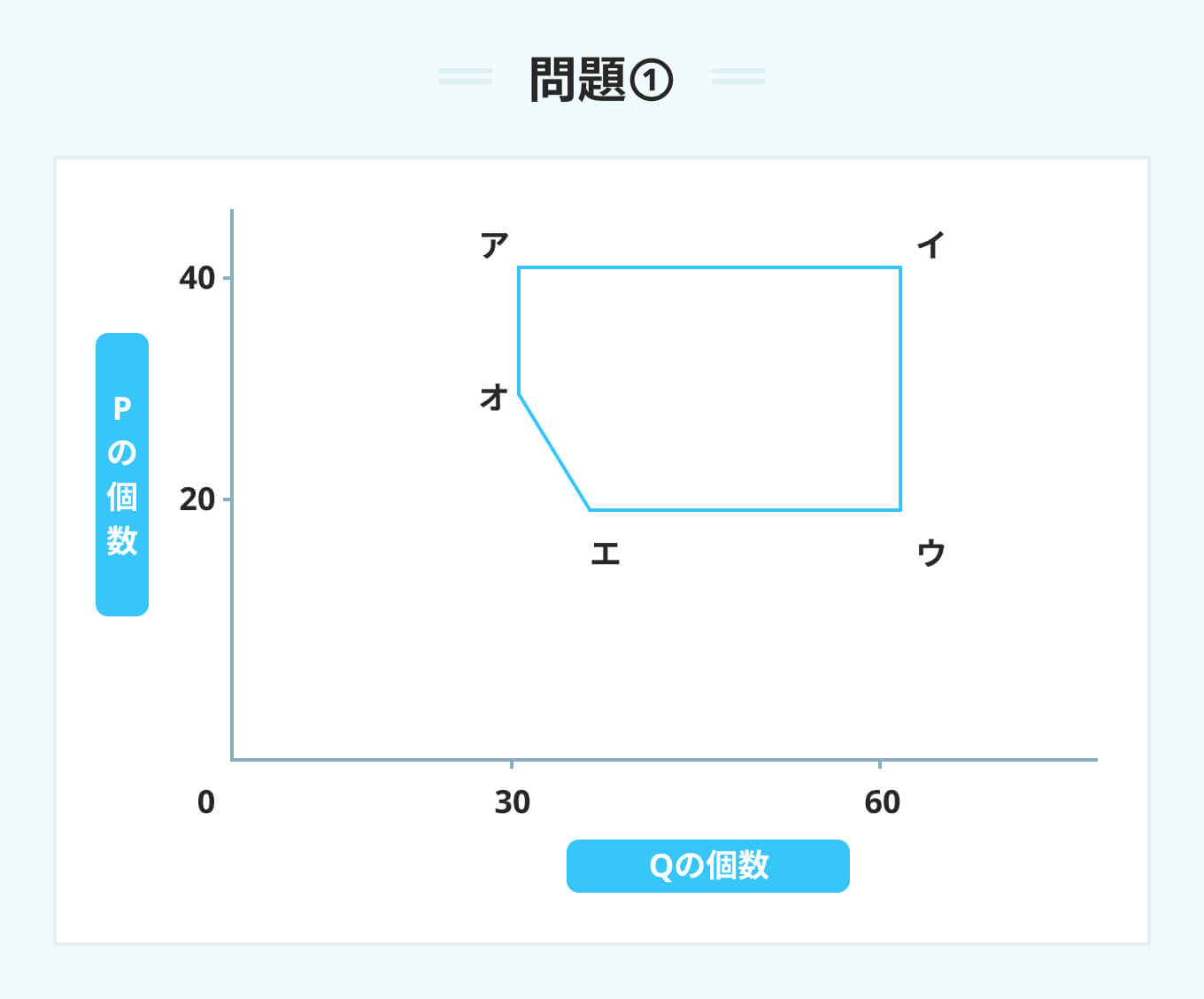
ある工場では製品の部品として、部品Pと部品Qを定期的に購入している。それぞれの購入量は、次の5つの条件によって決められている。 条件a：部品Pは20個以上である。 条件b：部品Pは40個以下である。 条件c：部品Qは30個以上である。 条件d：部品Qは60個以下である。 条件e：部品Pと部品Qの合計は60個以上である。 これらの条件を満たす購入量の範囲は、図のア、イ、ウ、エ、オで囲まれた五角形の領域で表される。 点オと点エを通る直線で表される境界は、a～eのどの条件によるものか。
選択肢
正解：E
グラフの縦軸は部品Pの個数、横軸は部品Qの個数を表している。点オと点エを結ぶ線は、グラフの左下にある斜めの線である。
各条件を境界線として整理すると、条件a（Pは20個以上）は下の水平な線、条件b（Pは40個以下）は上の水平な線、条件c（Qは30個以上）は左の垂直な線、条件d（Qは60個以下）は右の垂直な線となる。
点オと点エを通る線は、PとQの合計が60個（P+Q=60）となる境界を示しているため、条件eに該当する。
「点オと点エを通る直線」が、グラフの軸に対して斜めになっていることにまず注目しましょう。
軸はそれぞれ縦軸が部品Pの個数、横軸は部品Qの個数を表しているため、「直線が斜めになる条件」とは「部品Pと部品Qの個数が、なんらかの関係で影響し合っている」と類推されます。
あとは条件文の中に部品Pと部品Qが両方とも出てくるものを探せば、簡単に正解を絞り込むことができます。
問題2（難易度：★★★☆☆）
問題
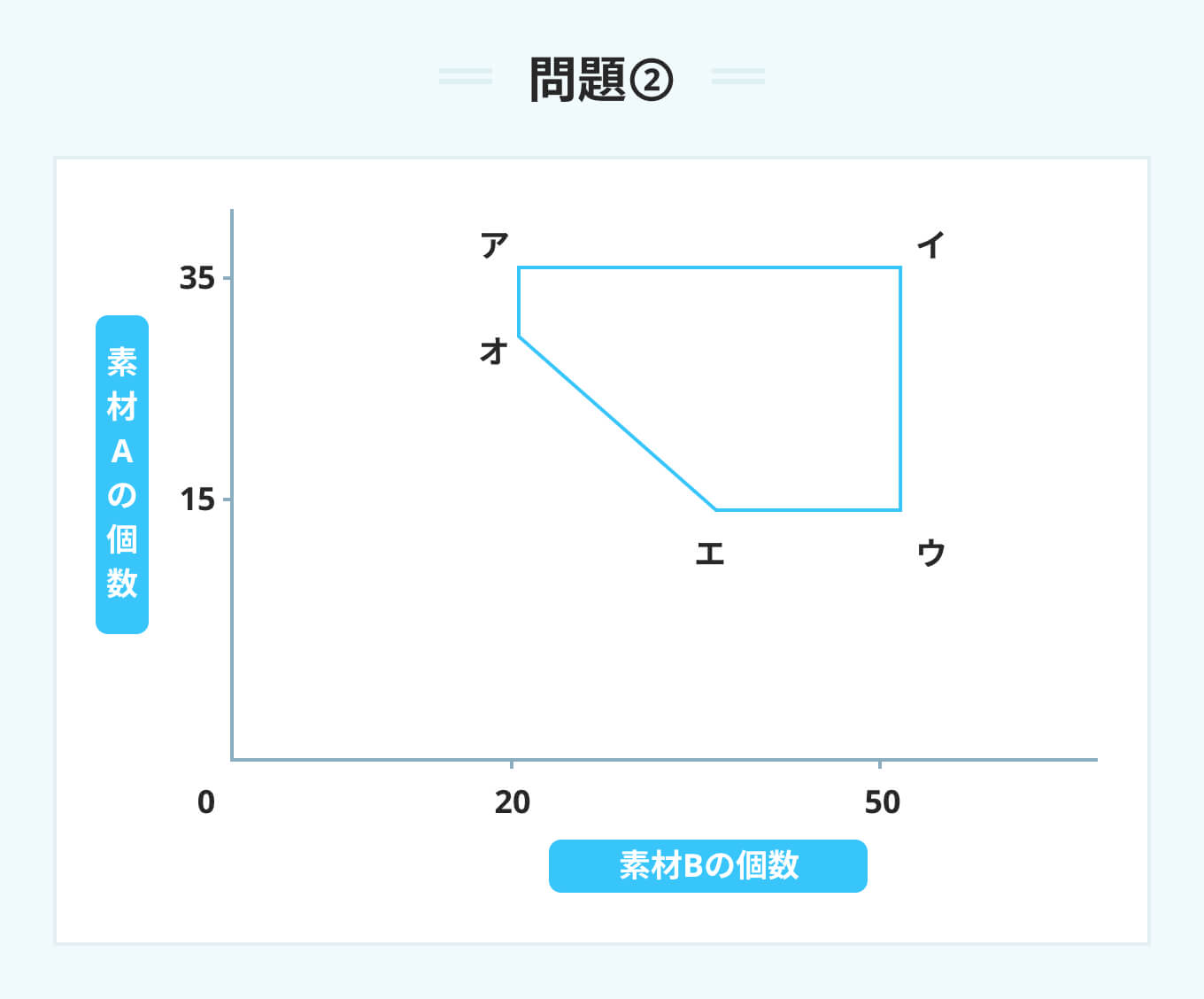
ある商社では原料として、素材Aと素材Bを仕入れている。素材Aの価格は1個当たり400円、素材Bの価格は1個当たり300円である。1回に仕入れる量は、次の5つの条件で決められている。 条件a：素材Aは15個以上である。 条件b：素材Aは35個以下である。 条件c：素材Bは20個以上である。 条件d：素材Bは50個以下である。 条件e：素材Aと素材Bの合計が50個以上である。 これらの条件を満たす仕入れ量の範囲は、図の点ア、イ、ウ、エ、オで囲まれた領域で表される。 仕入れにかかる費用の総額が最も安くなるのは、素材A、素材Bの個数を、図の点ア〜オのどの点の組み合わせで購入したときか。
選択肢
正解：D
仕入れにかかる費用の総額を最も安くする点を探す。費用は「400×素材Aの個数＋300×素材Bの個数」で計算される。
費用を安くするためには、仕入れ個数が少ない原点に近い点を確認すれば良い。合計個数が50個となる条件eの境界線上にある点エ（A＝15、B＝35）と点オ（A＝30、B＝20）を比較する。
単価の高い素材Aを最小の15個に抑えた点エの方が、点オよりも費用が1,500円安くなるため、正解はエとなる。
「仕入れにかかる費用が最も安くなる」という言葉に注目しましょう。
単純に考えると、素材の数は「少ない」ほど、素材の単価は「安い」ほど、仕入れの費用は安くなるはずです。つまり、グラフでいうと原点に近ければ近いほど（素材の仕入れ数が少ないほど）、費用は安くなります。
この時点で、おおよその正解が推測できます。このように、計算する前に選択肢を絞り込むことで時短が可能です。
問題3（難易度：★★☆☆☆）
問題
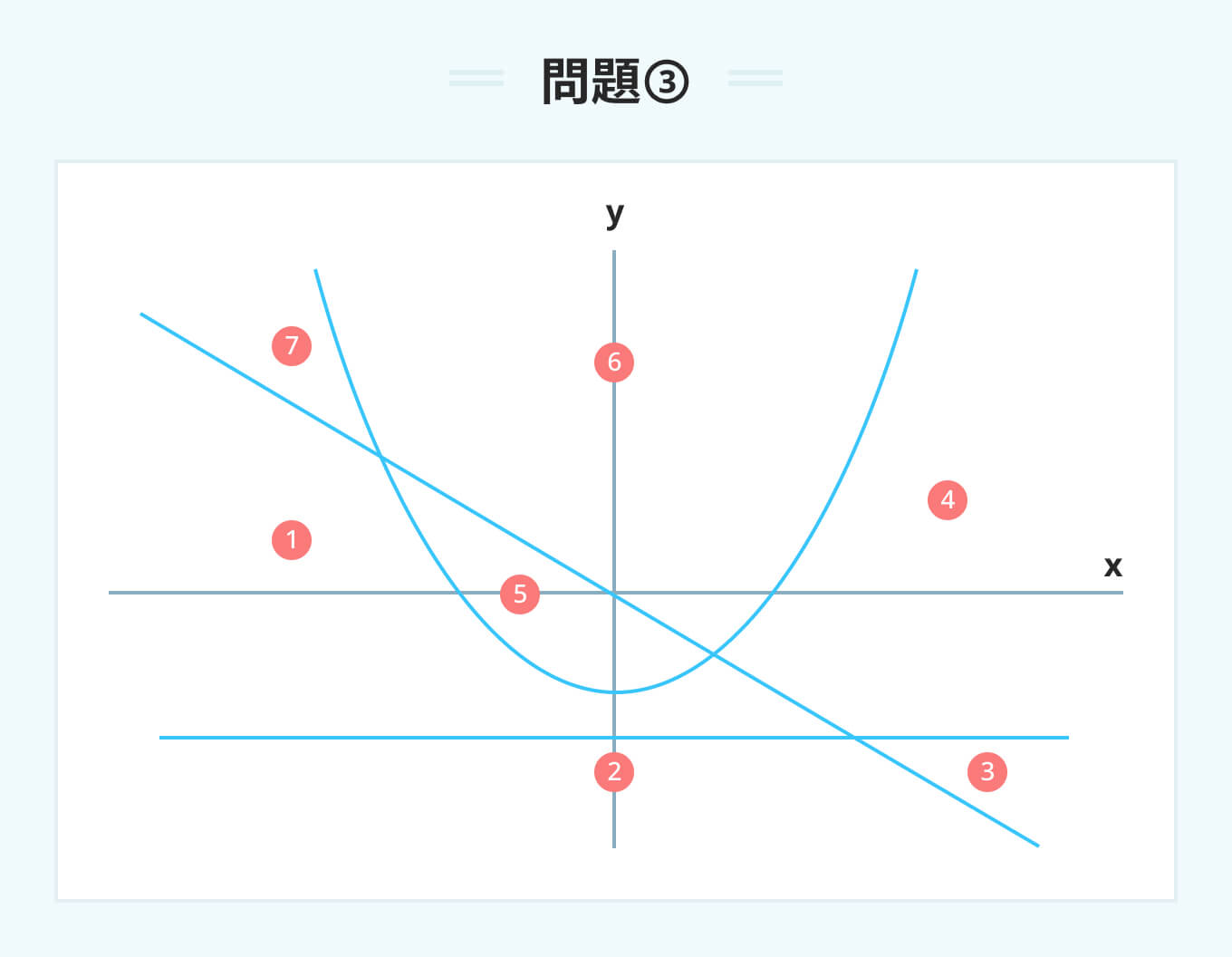
次の3つの式によって表される放物線と直線は、図のように平面を7つの領域に分ける。 ア y=x^2-1 イ y=-2x ウ y=-2 これらの領域は、上のア、イ、ウの各式の等号をそれぞれ不等号に置き換えた、1つずつの連立不等式によって表される。 ア、イ、ウの式の等号を、すべて不等号に置き換えて、⑤の領域を表すとき、左開きの不等号（>）がつくのは、ア、イ、ウのうちどれか。
選択肢
正解：D
領域が各式のグラフよりも上側にあるときy>式の右辺、下側にあるときy<式の右辺となる。
領域⑤は、放物線（ア）の上なのでy>x^2-1、斜めの直線（イ）の下なのでy<-2x、水平な直線（ウ）の上なのでy>-2と表される。
よって、不等号が左開きなのはアとウ。
問題4（難易度：★★★☆☆）
問題
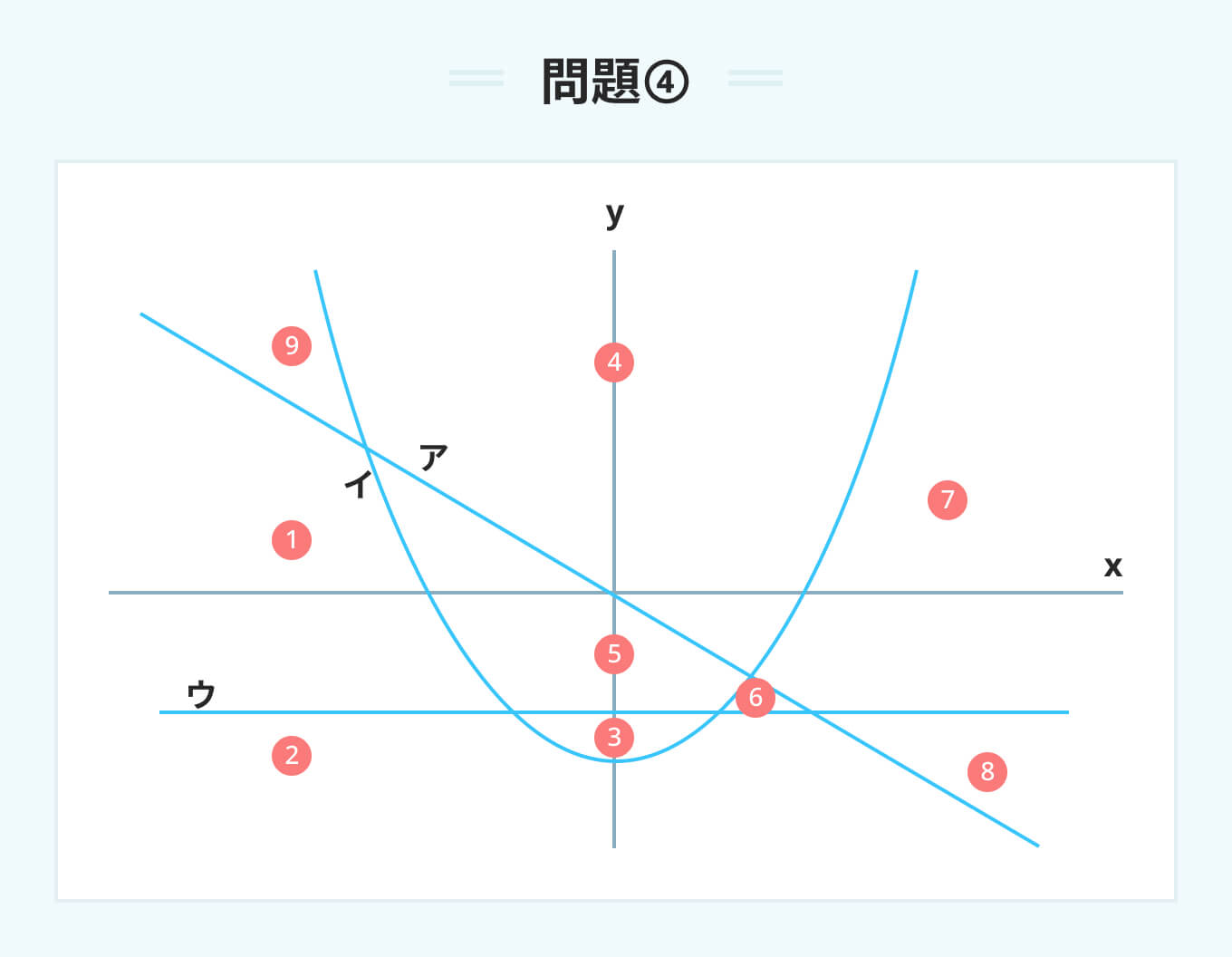
次の3つの式によって表される放物線と直線は、図のように平面を8つの領域に分ける。 ア y=x^2-4 イ y=-2x ウ y=-3 これらの領域は、上のア、イ、ウの各式の等号をそれぞれ不等号に置き換えた、1つの連立不等式によって表される。 次の連立不等式によって表される領域は、①から⑧のうちのどれか。 ア y>x^2-4 イ y<-2x ウ y<-3
選択肢
正解：B
与えられた3つの不等式の条件を整理し、共通する領域を特定する。
条件1：y>x^2-4 放物線よりもyの値が大きい、つまり放物線の上側の領域を指す。外側にある①、②、⑦、⑧などは除外される。
条件2：y<-2x 斜めの直線よりもyの値が小さい、つまり直線の下側の領域を指す。直線よりも上にある①、④、⑦などは除外される。
条件3：y<-3 水平な直線よりもyの値が小さい、つまり直線の下側の領域を指す。直線の上側にある②、④、⑤、⑥などは除外される。
これらすべての条件を満たす場所は、放物線の内側であり、かつ2本の直線よりも下にある領域③となる。
このような問題は、「グラフの形」のパターンを認識することからマスターするのが重要です。
「y=◯x^2」が入っている場合は「放物線」（xの係数がプラスなら下に凸、マイナスであれば上に凸）
「y=◯x」の式の場合は「斜めの直線」
「y=◯」の式の場合は「軸に平行な直線」
という形を、反射的に想像できるようにしましょう。
問題5（難易度：★★★★☆）
問題
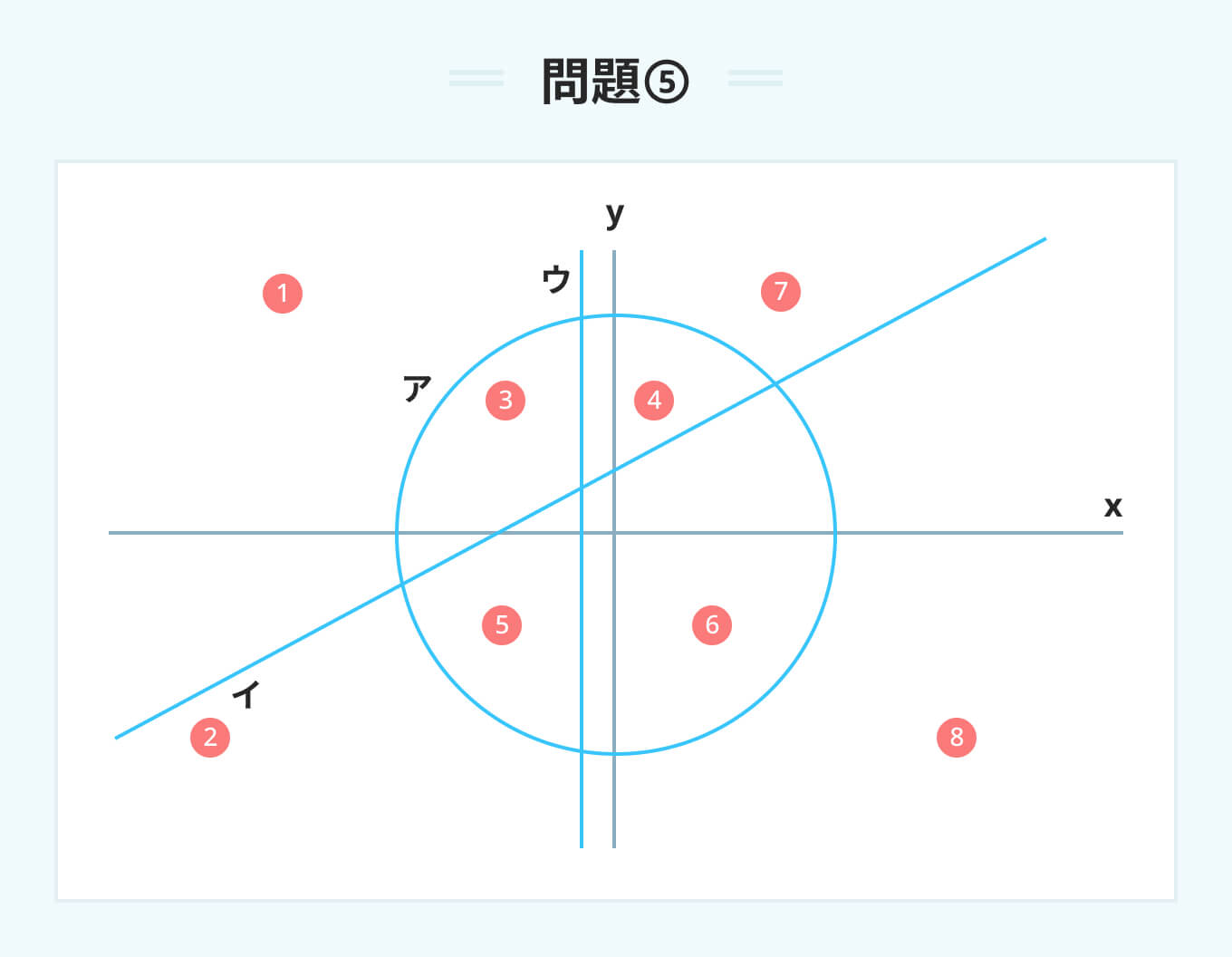
ア、イ、ウの3つの式によって示される円と直線は、図のように平面を①から⑧まで8つの領域に分ける。 ア x^2+y^2=36 イ y=x+1 ウ x=-2 これらの領域は、ア、イ、ウの3つの式の等号を適宜不等号に置き換えて得られる1組の連立不等式によって示される。 ア、イ、ウの式の等号をすべて不等号に置き換えて、色がついた領域（図の塗りつぶされた部分）を表したときに、右開きの不等号（＜）がつくのは、ア、イ、ウのうちどれか。
選択肢
正解：D
図の色がついた領域が、それぞれのグラフに対してどのような位置にあるかを確認する。
ア：円（x^2+y^2=36）について、領域は円の内側にある。円の内側は半径の二乗より小さい範囲を示すため、不等号は＜（右開き）となる。
イ：直線（y=x+1）について、領域はこの直線よりも下側に位置している。yの値が直線の式よりも小さくなるため、不等号は＜（右開き）となる。
ウ：直線（x=-2）について、領域は直線よりも右側にある。xの値は-2より大きくなるため、不等号は＞（左開き）となる。
したがって、右開きの不等号（＜）がつくのはアとイである。
グラフに円を描くことのできる式（x^2+y^2=◯）を想像できるかが大きなポイントになります。円型のグラフも頻出ですので、きちんとマスターしましょう。
式が不等号の場合、円の「内側」を指すのは不等号が右開きの場合（x^2+y^2＜◯）であることを、事前に頭に入れておけば解答スピードが速まります。
問題6（難易度：★★★★★）
問題
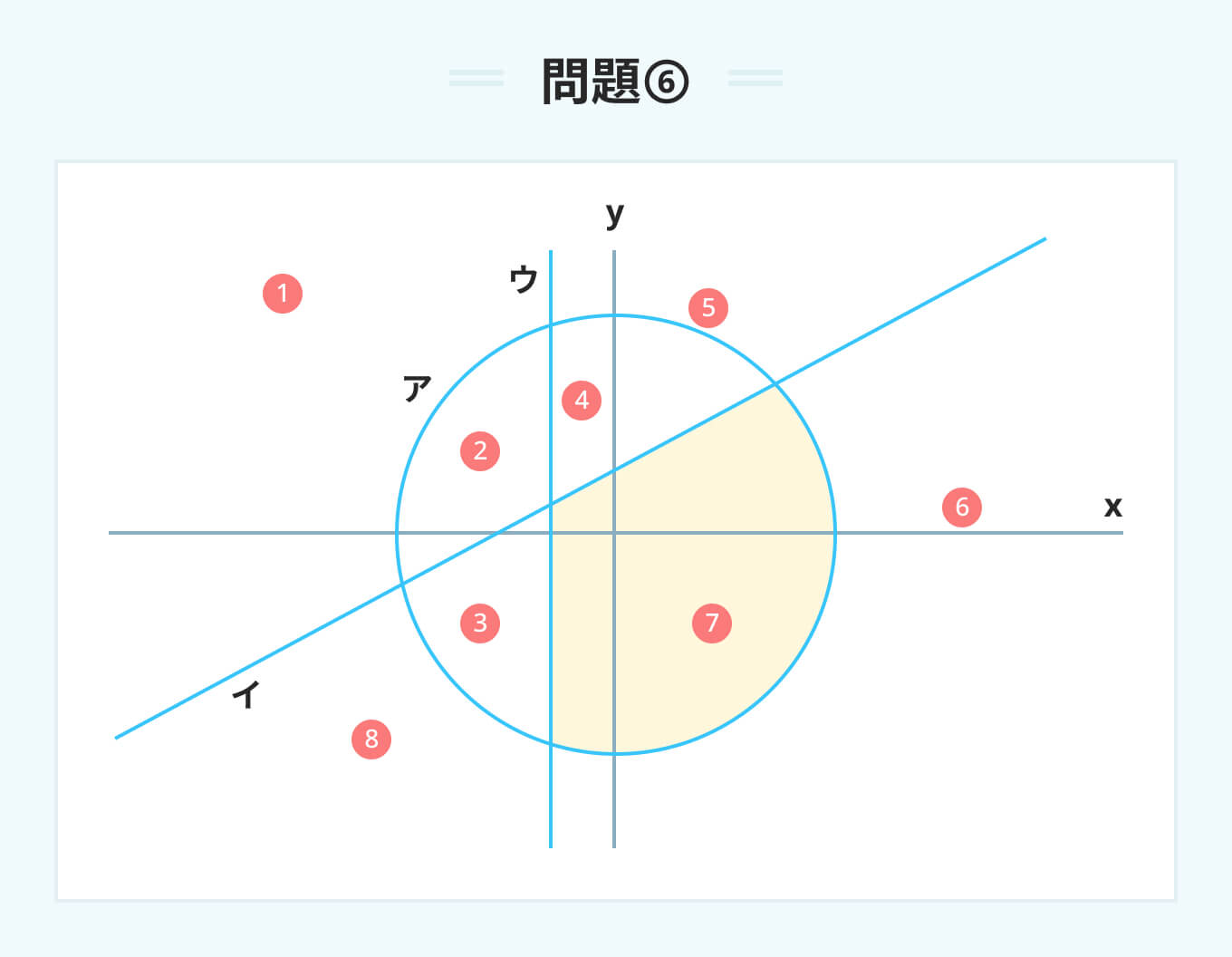
ア、イ、ウの3つの式によって示される円と直線は、図のように平面を①から⑧までの8つの領域に分ける。 ア x^2+y^2=36 イ y=x+2 ウ x=-1 これらの領域は、ア、イ、ウの3つの式の等号を適宜不等号に置き換えて得られる1つの連立不等式によって示される。 次の3つの式からなる連立不等式によって表される領域はどこか。 カ x^2+y^2<36 キ y>x+2 ク x>-1
選択肢
正解：C
与えられた連立不等式の条件を1つずつ確認し、該当する領域を特定する。
条件カは、円の方程式の右辺よりも小さいため、円の内側の領域を指す。この条件により、円の外側にある①、②、⑦、⑧は除外される。
条件キは、yの値が直線の式より大きいため、直線の上側の領域である。
条件クは、xの値が-1より大きいため、垂直な直線の右側の領域である。
これら3つの条件をすべて満たすのは、図の領域④である。
練習問題が解けたら、次はSPI模試に挑戦して実力をチェックしてみましょう。
SPI「グラフの領域」を対策する際のポイント
SPIの非言語に関する記事
◇非言語の対策
SPI非言語は対策すれば怖くない！ 出題傾向や例題を徹底解説
SPIに関する記事
◇解答時間
SPIの解答時間を受検方式別に解説！ 時間切れを防ぐコツ10選も
◇勉強法
効率抜群なSPIの勉強法｜出題形式と頻出問題を踏まえた対策を伝授
◇勉強時間
SPIの勉強時間をプロが解説！ おすすめの進め方や重点ポイントも
グラフの領域以外の練習問題も解いてみよう！
SPIは多くの分野に分かれています。練習問題を繰り返し解いて、苦手を攻略しましょう。
各分野の問題が解けたら、最後にSPI模試に挑戦してみましょう。
執筆・編集 PORTキャリア編集部
明日から使える就活ノウハウ情報をテーマに、履歴書・志望動機といった書類の作成方法や面接やグループワークなどの選考対策の方法など、多様な選択肢や答えを提示することで、一人ひとりの就活生の意思決定に役立つことを目指しています。 国家資格を保有するキャリアコンサルタントや、現役キャリアアドバイザーら専門家監修のもと、最高品質の記事を配信しています。
＞ コンテンツポリシー
記事の編集責任者 熊野 公俊 Kumano Masatoshi
高校卒業後、航空自衛隊に入隊。4年間の在籍後、22歳で都内の大学に入学し、心理学・教育学を学ぶ。卒業後は人材サービスを展開するパソナで、人材派遣営業やグローバル人材の採用支援、女性活躍推進事業に従事。NPO（非営利団体）での勤務を経て、「PORTキャリア」を運営するポートに入社。キャリアアドバイザーとして年間400人と面談し、延べ2500人にも及ぶ学生を支援。2020年、厚生労働大臣認定のキャリアコンサルタント養成講習であるGCDF-Japan（キャリアカウンセラートレーニングプログラム）を修了
アドバイザーからワンポイントアドバイス数式と紐づくグラフの形を覚えることで正答率は上がる
国家資格キャリアコンサルタント／2級ファイナンシャル・プランニング技能士
山田 圭佑
プロフィールを見る「グラフの領域」の問題を解くためには、問題中に示されたグラフの形の読み取りや、数式をもとにして頭の中でグラフを描く想像力が必要になるため、1問あたりにかける時間は長くなりがちです。
しばらく考えても答えがわからない場合は、諦めて次の問題に進んでしまうことも考えましょう。
数式を見た瞬間にグラフが頭に浮かぶようにしよう
確実に得点を稼ぐためには、下記の頻出のグラフの形と、それの元になる数式の形式をしっかりと頭にインプットすることが大切です。
①軸と平行な直線（定数）
②軸に対して斜めの直線（1次関数）
③軸に対しての放物線（2次関数）
④円（2次関数の応用）
数式を見た瞬間にグラフの形が、またグラフを見た瞬間に数式の概要が頭に浮かんでくるまでマスターしていきましょう。