SPIの「速度算」は非言語分野で出題されます。与えられた情報から速度、時間、距離を求める問題が中心です。
この記事では、Webテストの支援経験を持つキャリアコンサルタントの西さんとともにSPIの「速度算」の解き方について解説していきます。具体的な対策方法についても解説しているので、「速度算」に苦手意識がある人は参考にしてみてください。
記事の後半では「速度算」の練習問題を20問紹介しています。さまざまな出題パターンを網羅的に解説しているので、ぜひSPIの対策に役立ててください。
よりSPIの本番をイメージして対策したい人は、SPI対策模試にも挑戦してみてください。
SPI「速度算」の概要
- 問題パターン:旅人算、平均速度を求める問題、通過算など
- 1問あたりの時間:1分程度
- 形式ごとの出題頻度:テストセンター(中)ペーパーテスト(高)Webテスティング(中)
- 速度算の解き方をわかりやすく教えてください!
基本的な公式+単位の変換が攻略のカギ
速度算を解く前に、基本的な公式(はじき)を覚えておく必要があります。
次に、設問を読んだときに、単位の変換が必要な問題が多いことに気付いてください。
「時速〇kmで何分かかるか」や「時速〇kmで〇mの~」のように、「時と分(または秒)」や「kmとm」のように単位が不揃いになっていることが多いので、単位を揃えずにそのまま計算するとミスが生じます。基本的には、「分」や「m」で揃える意識を持ってください。
そして、速度算は1問あたり、1分程度で解けるように練習しましょう。
「速度算」を解くうえで必須の「は・じ・き」の公式
速度・距離・時間の関係
- ①速さ=距離/時間
- ②時間=距離/速さ
- ③距離=速さ×時間
以下のような図で覚えると覚えやすいです。
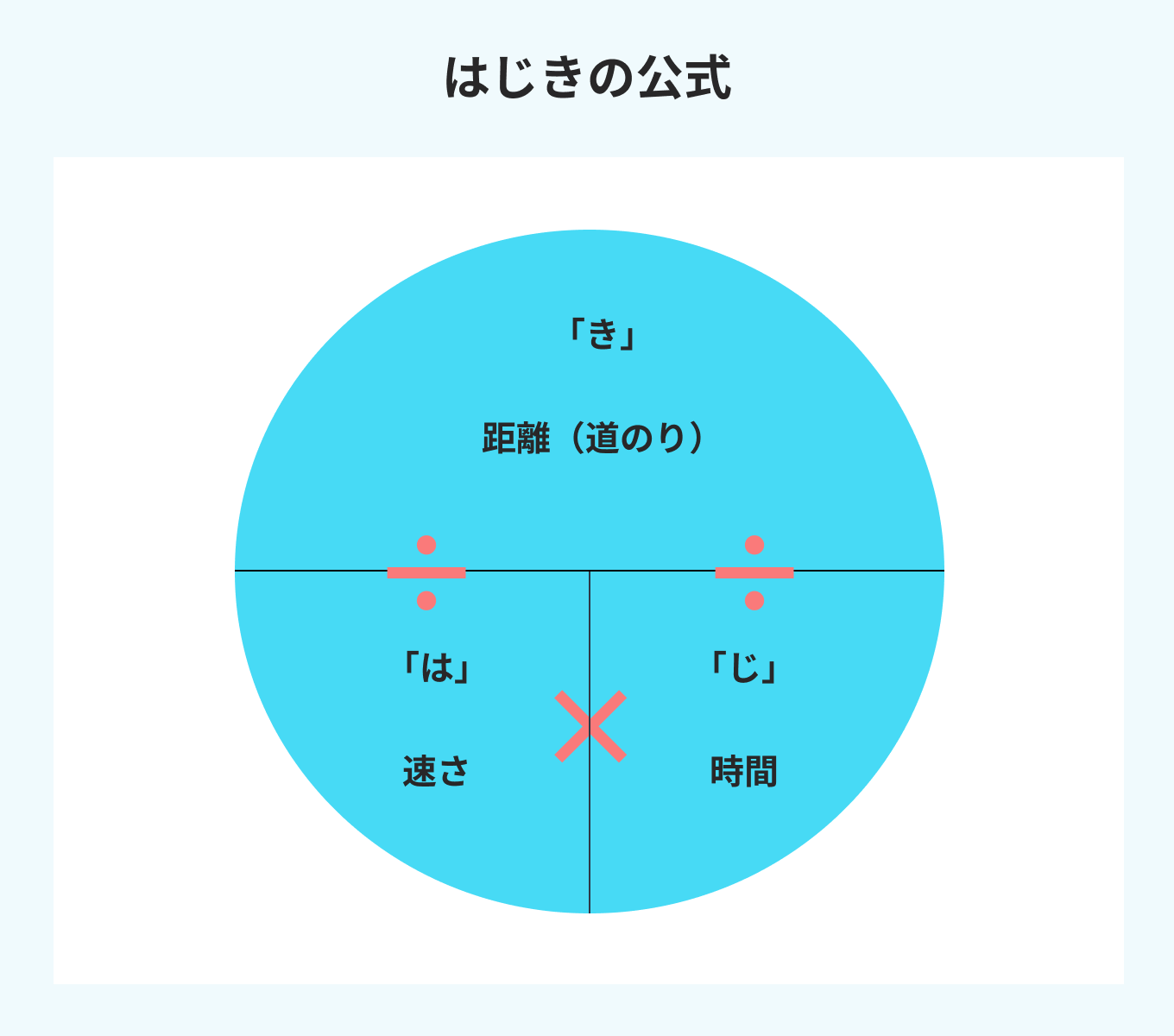
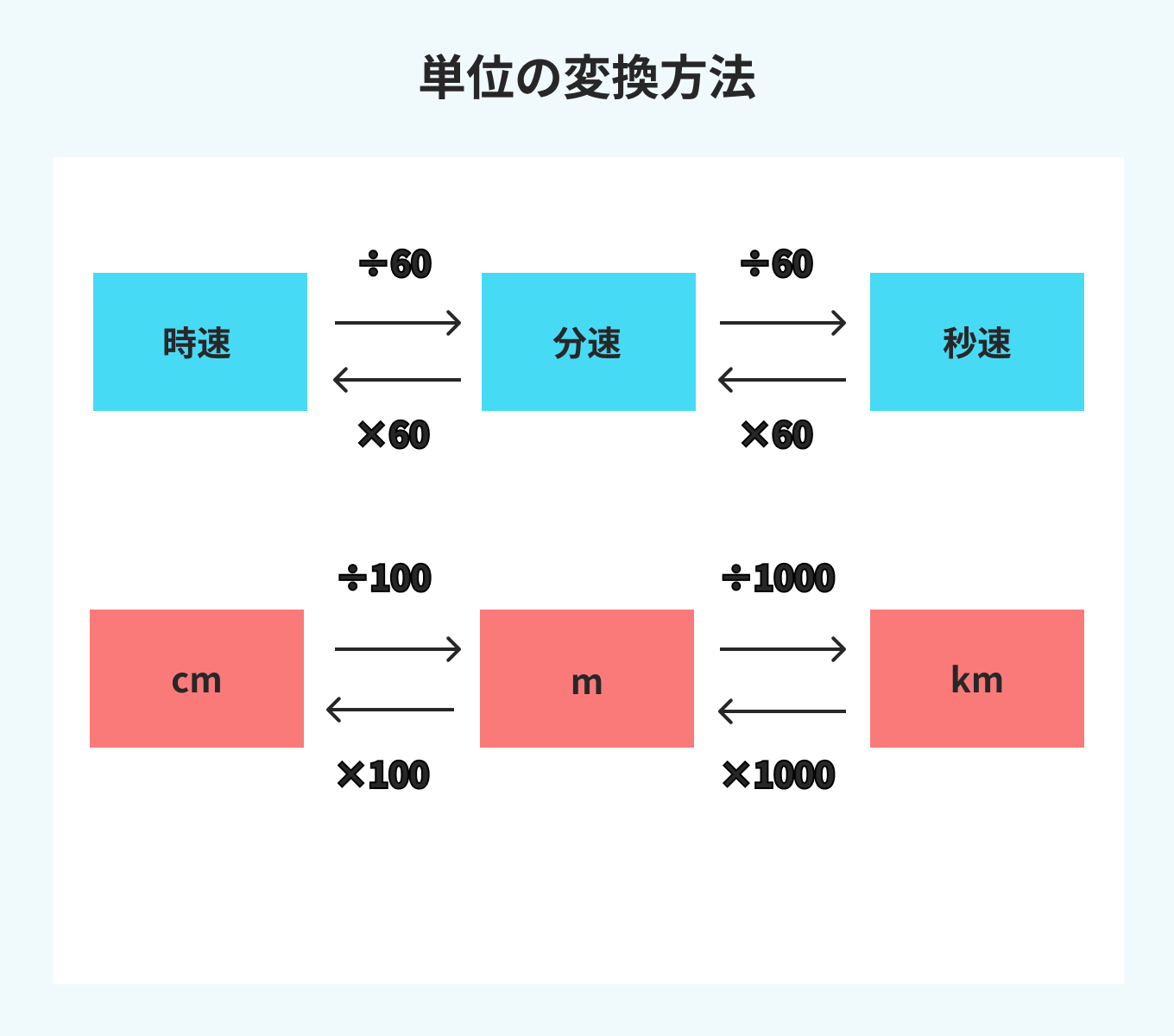
覚えておこう! 単位の変換一覧
単位の変換が即座にできると問題を解く時間が短縮できます。時間と距離では変換方法が違うので気を付けましょう。
SPI「速度算」の練習問題20問|西さんによる解き方の解説付き!
SPI「速度算」の練習問題を解説付きで20問紹介します。必要な公式はどれなのか素早く見つけるためには演習が不可欠です。ぜひ最後まで問題を解いてみて、速度算を解く感覚をつかんでいきましょう。
速度算の解き方に不安がある人は、まず「問題を解く前に確認! 速度算の解答のコツ」を一読してみてください。その後の理解度が大きく変わりますよ。
問題1(難易度:★☆☆☆☆)
問題
営業部の田中さんが分速75mで会社を出て営業先に向かった。その12分後に、田中さんが資料を忘れていることに気づいた後輩が、分速225mの自転車で田中さんを追いかけた。後輩が出発してから何分後に田中さんに追いつくか求めよ。
選択肢
正解:C
後輩が出発してからx分後に田中さんに追いつくとする。
後輩が田中さんに追いつくのは、最初の12分を含めた田中さんの移動距離と後輩の移動距離が等しくなるときである。
x分後の田中さんの移動距離:(12分+x分)×75m/分
後輩の移動距離:x分×225m/分
75(12+x)=225x、900+75x=225x、150x=900、x=6。
よって、後輩は出発してから6分後に田中さんに追いつく。
いわゆる「追いつき算」です。
追いつき算では、最初に出発した人(田中さん)が最終的に進んだ距離を、「最初の12分間で進んだ距離」と「後輩が出発してから、追いつくまでに進んだ距離」の合計としてとらえることがポイントとなります。
そこで、後輩が出発して追いつくまでの時間をX分とすると、田中さんは追いつかれるまでに、12分+X分を分速75mで進んだことになるのです。
問題2(難易度:★☆☆☆☆)
問題
東西に伸びる1.5kmの一本道がある。西端からAさんが分速70mで、東端からBさんが分速80mで、同時に向かい合って歩き出した。2人が出会うのは出発してから何分後か求めよ。
選択肢
正解:C
向かい合って進む場合、2人の距離は「2人の速さの和」で縮まっていく。
①単位をそろえる
距離がkm、速さがm(メートル)になっているため、距離をmに直す。
1.5km=1500m
②相対速度(速さの和)を求める
互いに近づくため、速さを足す。
70+80=150(m/分)
③時間を求める
時間=距離÷速さ
1500÷15=10
よって、10分後に出会う。
いわゆる「出会い算」です。
出会い算のポイントは、二人の速さを「足す」ことにあります。その際、今回の問題のように、単位が異なる場合がありますので、「単位をそろえる」ことを意識してください。問題をよく見てみると、距離はkmであるのに対して、二人の速度はmを用いていますよね。
どちらかの単位に揃える必要がありますが、mをkmにすると小数点が出ることがあるので、kmをmに直すのが楽です。
問題3(難易度:★☆☆☆☆)
問題
本社と支社は2.8km離れている。本社から社員Xが分速75mで、支社から社員Yが分速65mで、同時に出発して互いの会社へ向かった。2人がすれ違うのは出発してから何分後か求めよ。
選択肢
正解:D
距離の和を相対速度で割って求める。
単位を揃える2.8km=2800m
相対速度(速さの和)を求める75+65=140(m/分)
時間を求める2800÷140=20
よって、20分後にすれ違う。
「出会い算」の計算パターンは単純です。「何分後か」、つまり時間を求めるので、「距離÷速さ」の公式に当てはめましょう。
ただし、この公式を用いる前に必ず単位を揃えるのを忘れないようにしてください。
焦って単位を揃えずに計算してしまうと正しい答えが出ないので、まずは単位を確認しましょう。
問題4(難易度:★☆☆☆☆)
問題
山頂への物資運搬のため、トラックで山道を往復した。行きは登り坂のため時速20km、帰りは下り坂のため時速30kmで走行した。このときの往復の平均速度は時速何kmか求めよ。
選択肢
正解:B
「往復の合計距離÷往復の合計時間」で求める。
①距離を仮定する
片道の距離を20と30の最小公倍数である60kmと仮定する。
②かかる時間を求める
行き:60km÷20km/h=3時間
帰り:60km÷30km/h=2時間
往復の合計時間は3+2=5時間である。
平均速度を計算する往復の距離は
60×2=120km。
120km÷5時間=24km/h
よって、平均速度は時速24kmである。
速度を単に足して2で割る(20+30)÷2=25は誤りである。
いわゆる「平均速度」を求める問題です。「速度」、つまり「速さ」を求める公式は、「距離÷時間」でしたね。
「行きは~」「帰りは~」とありますから、行きの距離と帰りの距離を足す必要があります。しかし、問題文には明確な距離が書かれていないので、「仮に」という形で、行き帰りの速度で表されている数値の最小公倍数を使いましょう。
この問題では20と30の最小公倍数で60を「片道」の距離と仮定します。「距離÷速度=時間」なので、一旦距離を60kmとした場合の行きと帰りにかかった時間を算出し、合計時間を出すことができるのです。
片道の距離を60kmとしているので、往復ではその2倍の120kmとなります。平均速度は「往復距離÷全体でかかった時間」で求めましょう。
問題5(難易度:★☆☆☆☆)
問題
A都市からB都市まで車で往復した。渋滞していた行きは時速40kmで進み、空いていた帰りは時速60kmで進んだ。 このときの往復の平均速度は時速何kmか求めよ。
選択肢
正解:B
①距離を仮定する
40と60の最小公倍数である120kmを片道の距離とする。
②かかる時間を求める
行き:120÷40=3時間
帰り:120÷60=2時間
合計時間は5時間。
平均速度を計算する往復距離は
120×2=240km。240÷5=48km/h
よって、時速48kmである。
「平均速度」は、「往復の距離÷全体でかかった時間」で求めることができます。
そのため、まずは「往復の距離」を決める必要がありますが、設問からは明確な距離が書かれていません。
そこで、仮の片道の距離を行きの速度と帰りの速度の最小公倍数とします。ここでは120kmで往復は240kmです。仮の片道の距離÷速度=片道にかかる時間になるので、行きと帰りにかかった時間をそれぞれ計算することで合計の時間を出すことができます。
最後に「往復の距離(240km)÷往復でかかった時間(5時間)」で答えを導き出しましょう。
問題6(難易度:★☆☆☆☆)
問題
ある区間を特急列車で往復する実験を行った。行きは時速120km、帰りは時速180kmで走行した。 このときの往復の平均速度は時速何kmか求めよ。
選択肢
正解:B
①距離を仮定する
120と180の最小公倍数である360kmを片道の距離とする。
②かかる時間を求める
行き:360÷120=3時間
帰り:360÷180=2時間
合計時間は5時間。
平均速度を計算する往復距離は
360×2=720km。720÷5=144km/h
よって、時速144kmである。
(選択肢Cの150km/hは単純平均の誤答)
「平均速度」を求める計算は、次の公式に当てはめます。「(片道の仮の距離×2)÷かかった往復の時間」です。
片道の距離が出ていないので、行きと帰りの速度の最小公倍数をいったん仮の片道の距離とします。ここでは360kmです。360km進むのに行きと帰りでそれぞれどのくらいの時間がかかったのかを計算し、合計します。
そして、往復の距離(ここでは360×2)÷往復に要した時間で計算すると、平均速度を算出できますよ。
問題7(難易度:★★☆☆☆)
問題
A君が分速90mで歩いて公園に向かった。A君が出発してから20分後に、A君の兄が分速210mで走って同じ道を追いかけた。 兄が出発してから何分後にA君に追いつくか求めよ
選択肢
正解:C
A君の兄(以降、兄)が出発してからx分後にA君に追いつくとする。
兄がA君に追いつくのは、最初の20分を含めたA君の移動距離と兄の移動距離が等しくなる時である。
x分後のA君の移動距離:(20分+x分)×90m/分
兄の移動距離:x分×210m/分
90(20+x)=210x、1800+90x=210x、120x=1800、x=15。
よって、兄は出発してから15分後にA君に追いつく。
ポイントは兄が出発する前にA君がある程度の距離を進んでいることに気付けるかどうかです。
A君は分速90mで20分歩いていて、さらに兄が追いつくまでさらに何分か(ここではX分とする)歩いているわけですから、A君は分速90mで最初の20+X分歩いていることになるので注意しましょう。
問題8(難易度:★★☆☆☆)
問題
サイクリングロードの南端と北端は4.8km離れている。南端から自転車に乗ったCさんが分速250mで、北端から徒歩のDさんが分速70mで、同時に向かい合って出発した。2人が出会うのは出発してから何分後か求めよ。
選択肢
正解:C
距離の和を相対速度で割って求める。
単位を揃える4.8km=4800m
相対速度(速さの和)を求める250+70=320(m/分)
時間を求める4800÷320(ゼロを消して480÷32を計算する)480÷32=15
よって、15分後に出会う。
この問題も「出会い算」です。解き方は「距離÷(二人の速さの和)」です。
kmとmが混じり合っているので、まずは単位をそろえましょう。kmは1000倍することでmになおすことができます。
問題が「何分後か」と「分」で質問しているので、分速に合わせてmにしておきます。単位が複数出てくるときはまずは揃えることを意識しましょう。
問題9(難易度:★★☆☆☆)
問題
全長140mの貨物列車が、時速90kmで走行している。この列車が長さ860mのトンネルに入り始めてから、完全に出るまでにかかる時間は何秒か。
選択肢
正解:D
通過算の基本通り、総距離を秒速で割って時間を求める。
①進むべき距離を求める。
「入り始め」から「完全に出る」までの距離は、トンネルの長さと列車の長さの和である。
860+140=1000(m)。
②速さの単位を変換する。
時速90kmを秒速(m/s)に直すため、3.6で割る。
90÷3.6=25(m/秒)。
③時間を求める
1000÷25=40(秒)。
よって、40秒かかる。
典型的な通過算の問題では、「貨物列車の長さ+トンネルの長さ」を計算します。なぜなら、この合計が貨物列車が移動した総距離になるからです。
また、もう一つのポイントが単位変換となります。設問は「何秒か」とありますが、時速は「時間」です。
「秒」と「時間」では単位が異なりますので、時速から秒速に変換するのを忘れないようにしましょう。
問題10(難易度:★★☆☆☆)
問題
長さ160mの快速電車が、時速108kmで走っている。この電車が全長1100mの鉄橋を渡り始めてから渡り終えるまでにかかる時間は何秒か。
選択肢
正解:D
①進むべき距離を求める。
1100 + 160 = 1260(m)。
②速さの単位を変換する。
108 ÷ 3.6 = 30(m/秒)。
③時間を求める。
1260 ÷ 30 = 42(秒)。
よって、42秒かかる。
選択肢A(36秒)は、電車の長さを足し忘れた場合の誤答(1100 ÷ 30)に近い値(約36.6)として配置している。
一般的に通過算では、「電車の長さ+鉄橋の長さ」を計算し、総距離を算出した後に、速度で割ります。
ただし、設問は「秒」で答える必要があるため、「時速」を「秒速」に計算し直す必要があるのです。
「時速÷3.6」を計算することで秒速を計算することが可能ですね。速度算では単位の変換が必須なので忘れてしまっている人は復習しておきましょう。
問題11(難易度:★★☆☆☆)
問題
駅からスタジアムまで、時速15kmで自転車をこぐと、時速9kmでジョギングをするよりも4分速く到着した。この時、駅からスタジアムまでの距離は何mか求めよ。
選択肢
正解:B
単位が「km/時」「分」「m」と混在しているため、「m/分」に統一して計算する。
①速さを分速(m/分)に変換する。
自転車:15(km/時)=15000(m)÷60(分)=250(m/分)。
ジョギング:9(km/時)=9000(m)÷60(分)=150(m/分)。
②方程式を立てる。
距離をxmとする。
「時間の差」が4分なので、以下の式が成り立つ。
(遅い方の時間)-(速い方の時間)=x/150-x/250=4。
計算する両辺に750(150と250の最小公倍数)を掛ける。
5x-3x=3000。2x=3000。x=1500。
よって、距離は1500mである。
「4分の差」を求めるには、「遅いほうの時間-速いほうの時間=4分」という式を立てましょう。
まず、求める距離をXmと置きます。次に単位をmと分に統一するため、時速を分速に変換します(1km=1000m、時速÷60=分速)。
時速15kmは分速250m(15000÷60)となり、かかる時間はX/250分です。一方、時速9kmは分速150m(9000÷60)となり、かかる時間はX/150分。これらを式に当てはめると「X/150-X/250=4」となります。
計算の際は、kmをmに、時間を分に直すこと、そして必ず「遅いほう(分母が小さいほう)から速いほうを引く」という手順を守ることが重要です。
問題12(難易度:★★☆☆☆)
問題
自宅から図書館まで行くのに、時速5.4kmで急いで歩くと、時速3.6kmで普通に歩くよりも5分早く着いた。この時、自宅から図書館までの距離は何mか求めよ。
選択肢
正解:C
時速に小数が含まれているが、手順は同じである。
m/分に直すと綺麗な整数になることが多い。
①速さを分速(m/分)に変換する。
急ぎ:5.4(km/時)=5400(m)÷60(分)=90(m/分)。
普通:3.6(km/時)=3600(m)÷60(分)=60(m/分)。
②方程式を立てる。
距離をxmとする。
x/60-x/90=5。
計算する両辺に180(60と90の最小公倍数)を掛ける。
3x-2x=900。x=900。
よって、距離は900mである。
目的は「距離を求める」ことですが、まずはそれぞれの時速でかかった時間を計算しましょう。
「時間=距離÷速さ」ですので、仮に距離をXmと置きます。
次にkmからmに単位を変換しましょう。3.6kmを1000倍して3,600m。これができれば、「1時間で3,600m、ということは1分当たりに進む距離は60で割れば求められるな」とわかりますよね。
つまり、時速3.6kmは、3600/60=分速60m。同様に時速5.4kmも分速に直し、「遅いほうの時間-速いほうの時間=5分」の式で計算しましょう。
問題13(難易度:★★☆☆☆)
問題
工場から物流センターまで荷物を運ぶ際、時速12.6kmで走行する電動カートを使うと、時速8.4kmで走行する台車を使う場合に比べて5分速く到着した。この時、工場から物流センターまでの距離は何mか求めよ。
選択肢
正解:C
数値がやや複雑だが、同様に単位変換をおこなう。
計算ミスに注意が必要である。
①速さを分速(m/分)に変換する。
電動カート:12.6(km/時)=12,600(m)÷60(分)=210(m/分)。
台車:8.4(km/時)=8,400(m)÷60(分)=140(m/分)。
②方程式を立てる。
距離をxmとする。
x/140-x/210=5。
③計算する両辺に420(140と210の最小公倍数)を掛ける。
3x-2x=2,100。x=2,100。
よって、距離は2,100mである。
設問では、「時速12.6km」「時速8.4km」「5分」のように、「時」と「分」が混ざっています。また、「12.6km」「8.4km」「何m」のように、kmとmも混ざっている状態です。
そのため、まずは単位をそれぞれmや分にそろえてあげましょう。
それができたら、今度はそれぞれの時速でかかった時間を計算してください。「時間」は「距離÷速さ」で計算できるため、距離をXとおいて計算するのが得策です。
問題14(難易度:★★☆☆☆)
問題
時速85kmで走る快速電車と、時速59kmで走る普通電車がすれ違う。快速電車の長さが160m、普通電車の長さが120mのとき、2つの電車がすれ違い始めてから完全にすれ違うのに何秒かかるか求めよ。
選択肢
正解:C
すれ違う場合、相対速度は2つの速さの和となる。
①相対速度を求める。
85+59=144(km/h)。
これを秒速に直すため、3.6で割る。
144÷3.6=40(m/秒)。
②移動距離(長さの和)を求める。
160+120=280(m)。
③時間を求める。
距離÷速さ=280÷40=7(秒)。
よって、7秒かかる。
典型的な「すれ違い算」の問題です。
すれ違い算の場合、距離は、それぞれの電車の長さの和です。また、速さもそれぞれの電車の速さの和になります。
つまり、「電車の長さの和÷電車の速さの和」を計算すれば、求める時間が算出されるということです。
問題15(難易度:★★☆☆☆)
問題
並行する線路を、秒速24mで走る長さ140mの列車Aと、同じ方向に秒速16mで走る長さ100mの列車Bが進んでいる。後方から来た列車Aが列車Bに追いついてから、完全に追い越すまでに何秒かかるか求めよ。
選択肢
正解:C
同じ方向に進んで追い越す場合、速さの差(相対速度)で、2つの列車の長さの和(距離)を縮めていくと考える。
①相対速度を求める。
同じ方向なので引き算をおこなう。
24-16=8(m/秒)。
これは、AがBを1秒間に8mずつ追い抜いていくことを意味する。
②追い越しに必要な距離を求める。
自分の長さと相手の長さの合計分だけ前に出る必要がある。
140+100=240(m)。
③時間を求める。
240÷8=30(秒)。
よって、30秒かかる。
「同じ方向に進んで、追いつき、追い越す」パターンの問題です。
列車Aの先頭が列車Bの最後尾に追いつき、そこから列車Aが列車Bの先頭と重なり、そして、最後には列車AがBを追い越す。つまり、このパターンではそれぞれの列車の長さの和を出すことが重要です。
逆に速度は両者の差を用いて計算し、最終的には「距離÷速度=時間」で答えを出します。
問題16(難易度:★★★☆☆)
問題
全長210mの特急列車が、時速126kmで走行している。この列車が長さ910mの橋を渡り始めてから渡り終えるまでにかかる時間は何秒か。
選択肢
正解:D
時速126kmという、3.6で割る際に暗算では少し手間取る数値設定にしており、計算力が問われる。
①進むべき距離を求める。
910+210=1120(m)。
②速さの単位を変換する。
126÷3.6=35(m/秒)。
③時間を求める
1120÷35=32(秒)。
よって、32秒かかる。
距離の和(1120)を速さ(35)で正確に割れるかがポイントである。
通過算ですが、なかでも計算が面倒なタイプの一つです。計算ミスをしないようにしましょう。
まず、「総距離(特急電車の長さ+橋の長さ)」を計算し、最後に「速さ」で割ります。正しい回答を導き出すには、時速を秒速に変える必要があるため注意が必要です。
問題17(難易度:★★★☆☆)
問題
全長220mの特急列車Aが時速110kmで、全長155mの急行列車Bが時速70kmで、互いに向かい合って走っている。2つの列車がすれ違い始めてから完全にすれ違うまでにかかる時間は何秒か。
選択肢
正解:C
計算手順は第1問と同様だが、距離の和や解答が小数になる点に注意が必要である。
①相対速度を求める。
110+70=180(km/h)。
②秒速に変換する。
180÷3.6=50(m/秒)。
③移動距離を求める。
220+155=375(m)。
④時間を求める。
375÷50=7.5(秒)。
よって、7.5秒である。
「すれ違い算」の計算ポイントは「それぞれの距離の合計÷それぞれの速度の合計」をすることです。
ただし、求めるのが「秒」であるため、時速を秒速に変換しなければなりません。時速÷3.6をすれば、秒速に変換されます。
また、mやkmが混じり合っているので、単位をmにそろえることを忘れないようにしましょう。小数点が出る問題では単位変換時に計算ミスをしやすいので、慎重に計算してください。
問題18(難易度:★★★☆☆)
問題
時速130kmの新快速電車(長さ250m)と、時速86kmの貨物列車(長さ182m)がすれ違う。2つの列車がすれ違い始めてから完全にすれ違うのに何秒かかるか求めよ。
選択肢
正解:A
数値が細かく、暗算での計算ミスが起きやすい設定となっている。
正確な筆算が求められる。
①相対速度を求める。
130+86=216(km/h)。
②秒速に変換する。
216÷3.6=60(m/秒)。
③移動距離を求める。
250+182=432(m)。
④時間を求める。
432÷60(43.2÷6と考えると計算しやすい)=7.2(秒)。
よって、7.2秒かかる。
「すれ違い算」では、「それぞれの電車・列車の長さの和÷それぞれの速度の和」で計算するのが基本です。
ただし、この手の問題は「単位がバラバラ」であるため統一する必要があります。
特に「時速」から「秒速」に変換するときには、「時速÷3.6」にしなければなりません。小数点が絡む計算ですから慎重におこなってください。
問題19(難易度:★★★☆☆)
問題
時速95kmで走行する全長240mの快速列車が、同じ線路の前方を時速41kmで走行している全長180mの貨物列車を追い越そうとしている。快速列車が貨物列車に追いついてから、完全に追い越すまでに何秒かかるか求めよ。
選択肢
正解:C
単位が時速(km/h)であるため、秒速(m/s)への変換が必要となる。
①相対速度を求め、単位を変換する。
速さの差は95-41=54(km/h)。
②これを秒速に直す(3.6で割る)。
54÷3.6=15(m/秒)。
③追い越しに必要な距離を求める。
240+180=420(m)。
④時間を求める。
420÷15=28(秒)。
よって、28秒かかる。
「同じ方向に進んで、追いつき、追い越す」パターンです。「列車同士の長さの和÷速度の差」で計算することで求めることができます。
ただし、単位が異なるため、単位をそろえましょう。km、m、時速、秒とあるため、基本的にはmと秒速で揃えたほうが計算ミスが少なくなります。
時速を秒速に直すためは、「時速÷3.6=秒速」という公式を使えば楽にできるので覚えておきましょう。
問題20(難易度:★★★☆☆)
問題
時速112kmで走る特急列車(長さ185m)が、同じ方向に時速85kmで走る回送列車(長さ130m)を追い抜く。特急列車の先頭が回送列車の最後尾に追いついてから、特急列車の最後尾が回送列車の先頭を完全に抜き去るまでにかかる時間は何秒か。
選択肢
正解:C
①相対速度を求め、単位を変換する。
速さの差は112-85=27(km/h)。
②秒速に直す。
27÷3.6=7.5(m/秒)。
③追い越しに必要な距離を求める。
185+130=315(m)。
④時間を求める。
315÷7.5=42(秒)。
よって、42秒かかる。
「同じ方向に進んで、追いつき、追い越す」パターンの問題です。
ただし、単位がバラバラなので(kmとm、時速と秒)、基本的にはmと秒速で揃えます。このとき、「時速÷3.6=秒速」という計算方法を知っておけば、時間を短縮できます。
「時間=距離÷速さ」ですから、距離は「列車同士の長さの和」、速さは「速いほう-遅いほう」で計算してください。
練習問題が解けたら、次はSPI模試に挑戦して実力をチェックしてみましょう。
専門家が教えるSPI「速度算」の対策ポイント
SPIの非言語に関する記事
◇非言語の対策
SPI非言語は対策すれば怖くない! 出題傾向や例題を徹底解説
SPIに関する記事
◇解答時間
SPIの解答時間を受検方式別に解説! 時間切れを防ぐコツ10選も
◇勉強法
効率抜群なSPIの勉強法|出題形式と頻出問題を踏まえた対策を伝授
◇勉強時間
SPIの勉強時間をプロが解説! おすすめの進め方や重点ポイントも
速度算以外の練習問題も解いてみよう!
SPIは多くの分野に分かれています。練習問題を繰り返し解いて、苦手を攻略しましょう。
各分野の問題が解けたら、最後にSPI模試に挑戦してみましょう。
執筆・編集 PORTキャリア編集部
> コンテンツポリシー
記事の編集責任者 熊野 公俊 Kumano Masatoshi














アドバイザーからワンポイントアドバイス学生が苦手な速度算のパターンは3つ存在する!
キャリアコンサルタント/西雄一教育研究所代表
西 雄一
プロフィールを見るまずは、設問を読んだときに、速度算の「種類」を見抜くことがポイントです。
速度算は大きく分けて
・平均速度を求める問題
・往復の時間の合計を求める問題
・追いつき/追い越しの問題
・すれ違いの問題
・通過(トンネル・橋)の問題
などに分類されます。
特に学生が苦手とするのが、「追いつき・追い越しの問題」「すれ違いの問題」「通過の問題」です。
どの単位で解答しなければならないのかを必ずチェックしよう!
「追いつき・追い越し」は「距離の差÷速度差」を意識しましょう。また、「すれ違いの問題」は「距離の和÷速度の和」となります。
そして、「通過の問題」は「(電車の長さ+トンネルの長さ)÷速度」です。「差を計算するのか」または「和を計算するのか」の判断が難しければ、イラストを描いて考えると良いでしょう。
この際に注意しなければならないのは、設問の「本当に求めたい答え」です。「何秒かかるのか」に対して、「時速〇km」でと書かれていれば「時速から秒速への変換(時速÷3.6)」をする必要があります。
速度算は小中レベルの問題ですが、対策本やアプリなどで数をこなして練習しましょう。