SPIの「集合」は非言語分野で出題されます。複数の集合の中から、与えられた条件に合致する人数を考える問題です。「ベン図」と呼ばれる簡易的な表を用いて情報を整理すると、スムーズに解くことができます。
この記事では、専門学校でのSPI指導経験を持つキャリアコンサルタントの田中さんとともにSPIの「集合」の解き方について解説していきます。
記事の後半には「集合」の練習問題を15問用意しています。少し複雑な応用問題も紹介しているので、「集合」に自信がある人もぜひ最後まで確認してみてくださいね。
よりSPIの本番をイメージして対策したい人は、SPI対策模試にも挑戦してみてください。
SPI「集合」の概要
- 問題パターン：2つの項目、3つの項目、全体の数を求める問題など
- 1問あたりの時間：1分～2分程度
- 形式ごとの出題頻度：テストセンター（高）ペーパーテスト（中）Webテスティング（高）
- 集合を解くときのコツをわかりやすく教えてください！
最初は「ベン図」を活用、慣れてきたら計算だけで処理しよう
SPIの「集合」は、中学～高校レベルの数学知識で解けるため、難易度自体は高くありません。しかし、テストセンターではほぼ確実に出題される最頻出分野であり、正答率が得点の伸びを左右するため、対策の優先順位は「最上位」と言えるでしょう。
攻略のカギは「スピード」です。最初は基本通り「ベン図」を描いて整理するのが確実ですが、本番ですべて図を描くと時間が足りません。
慣れてきたら図を描かずに、「計算式」だけで処理する応用テクニックを身に付けることが、ライバルに差をつけるポイントになります。
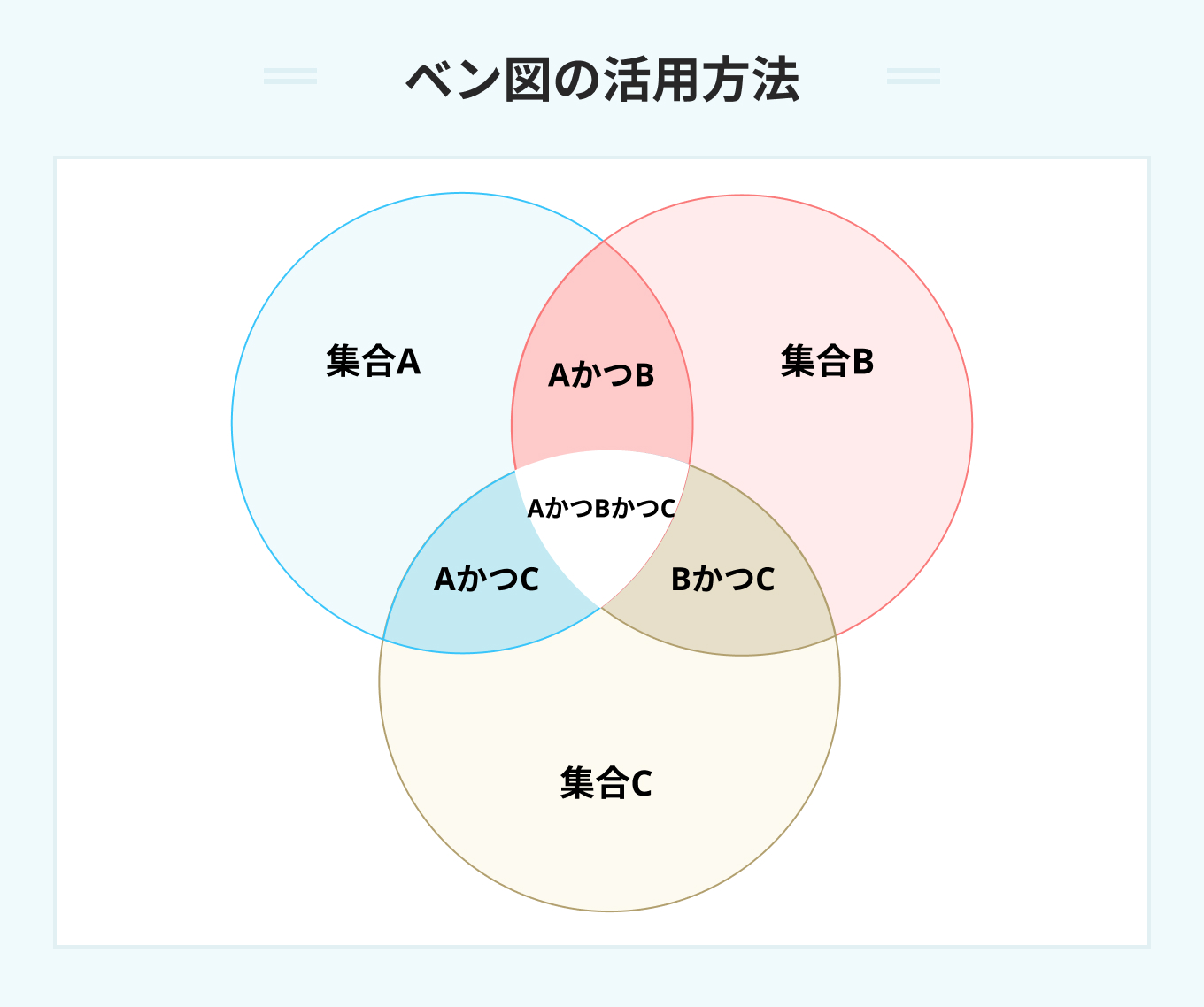
これで完璧！ ベン図の活用方法
集合の問題は複数の条件を与えられるため、慣れていないうちは頭の中だけで整理しようとすると混乱する恐れがあります。
集合を解く際は下記のようなベン図を用いて、与えられた情報を視覚的にわかりやすく整理するようにしましょう。
SPI「集合」の練習問題15問｜田中さんによる解き方の解説付き！
ここからは、SPI「集合」の練習問題を田中さんの解説付きで15問紹介します。項目が3つ以上にわたる問題などさまざまなパターンを解説しているので、ぜひ最後まで解いて自分の実力を確かめてみましょう。
また初めて「集合」の問題を解く人は、「問題を解く前に確認！ 集合の解答のコツ」を読んでから問題に着手するのがおすすめですよ。
問題1（難易度：★★☆☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある企業の従業員250人を対象に通勤手段の調査をおこなったところ、電車を利用している人が180人、バスを利用している人が95人いた。この中で、電車とバスの両方を利用している人は40人であった。
このとき、電車とバスのうちどちらか片方の手段だけを利用している人は何人か。
選択肢
正解：C
電車だけを利用している人と、バスだけを利用している人をそれぞれ求めて合計することで答えを求められる。
まず、電車を利用している180人のうち、40人はバスも利用している。したがって、電車「だけ」を利用している人は、180－40＝140（人）となる。
次に、バスを利用している95人のうち、40人は電車も利用している。したがって、バス「だけ」を利用している人は、95－40＝55（人）となる。
これらを足し合わせると、140＋55＝195（人）となる。
よって、正解は195人。
問題2（難易度：★★☆☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある企業の従業員400人を対象に調査をおこなったところ、普通自動車免許を持っている人が320人、自動二輪免許を持っている人が130人いた。また、どちらの免許も持っていない人が15人いた。
このとき、普通自動車免許と自動二輪免許の両方を持っている人は何人か？
選択肢
正解：C
まず、全体からどちらも持っていない人を引くことで、少なくとも一方の免許を持つ人の人数を求める。400-15=385（人）。
次に、普通自動車免許を持つ人と自動二輪免許を持つ人を合計する。320+130=450（人）。
この450人という数値は、両方の免許を持つ人を重複して数えている。したがって、単純な合計から免許を持つ人の数である385人を引くことで、重複している人数を求めることができる。450-385=65。
よって、65人。
集合の問題では文章を丁寧に追いすぎず、まず数値だけを拾うのがおすすめです。今回であれば全体が400、普通免許が320、二輪免許が130、どちらも無しが15ですね。
次に、「少なくとも一方」＝400−15を先に計算するのが時短のコツとなります。
320＋130は重複を二重に数えている合計なので、（320＋130）−（少なくとも一方）で両方の免許を所持している人の数を求めることができます。
問題3（難易度：★★☆☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある映画館で来場者150人を対象にアンケートをおこなった。その結果、アクション映画をよく見る人は95人、アニメ映画をよく見る人は60人であり、このうちアクション映画とアニメ映画の両方をよく見る人は30人であった。
このとき、アクション映画もアニメ映画もいずれもよく見ない人は何人か。
選択肢
正解：C
まず、アクション映画かアニメ映画の少なくとも一方を見る人の人数を求める。
これは、アクション映画を見る人とアニメ映画を見る人を足し合わせ、そこから重複して数えている「両方見る人」を引くことで求めることができる。95+60-30=125（人）。
全体の人数からこの人数を引けば、いずれも見ない人の人数を求めることができる。150-125=25。
よって、25人である。
「いずれもよく見ない」は補集合です。問題文を読むときは150、95、60、30と登場する4つの数値だけに印を付け、具体的なエピソードは流し読みで構いません。
手順は、少なくとも一方＝95＋60−30を出し、全体150から引くだけです。最後に「見ない人数」を答える問題であることをちゃんと確認してから解答すると、ケアレスミスを防ぐことができますよ。
問題4（難易度：★★☆☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある勉強会に参加した社会人100人を対象に、プログラミング学習と英語学習に取り組んでいるか調査をおこなった。プログラミングを学習している人は45人、英語を学習している人は35人いた。どちらの学習も取り組んでいない人が、両方の学習に取り組んでいる人の2倍の人数いたとする。
このとき、両方の学習に取り組んでいる人の人数はいくらか？
選択肢
正解：C
求めたい「両方の学習に取り組んでいる人数」をx人と置く。
問題文より「どちらも取り組んでいない人数」はその2倍なので、2xと表せる。
全体の人数である100人は、以下の式で表せる。
全体＝プログラミングの人＋英語の人－両方の学習の人（重複分）＋どちらも取り組んでいない人
これに数値を当てはめると、
100＝45＋35－x＋2xとなる。
式を整理すると
100＝80＋xとなり、x＝20とわかる。
よって、正解は20人。
条件文を読んですぐ、両方をx人、どちらも無しを2x人と置くことができるかがポイントです。
読むときは全体100、プログラミング45、英語35、倍率2倍と要点だけ拾えば十分です。
式を100＝45＋35−x＋2xと立て、整理してxを求めます。−xという、重複分を減らす手順を忘れないように意識してください。
問題5（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある展示会の来場者500人を対象にアンケートをおこなったところ、展示Aを見た人が300人、展示Bを見た人が180人、展示Cを見た人が150人いた。
展示Aと展示Bの両方を見た人が50人いて、かつ、展示Cだけを見た人が40人いたとすると、展示A、展示B、展示Cのいずれも見なかった人は何人か。
選択肢
正解：C
まず展示A〜Cを少なくとも1つ見た人の合計人数を求め、全体の人数から引く。
展示Aまたは展示Bを見た人数は、300＋180－50＝430（人）となる。
ここに、展示Aも展示Bも見ていない「展示Cだけ見た人」の40人を加える。展示Cだけ見た人は、手順1の430人とは重複しないため、そのまま足し合わせることができる。430＋40＝470（人）が、展示A〜Cを少なくとも1つ見た人の数だとわかる。
全体の500人から、この470人を引くと、500－470＝30となる。よって、30人。
3つの要素が出てきても、読むコツは一貫して「使う情報を絞る」こと。
拾うのはA.300、B.180、AかつB.50、Cだけ.40、全体.500の5点で十分です。まず「AまたはB＝300＋180−50」という式を作り、そこに「Cだけ.40」を足すことで「少なくとも1つ見た人数」がわかります。
最後に全体500から引けば、「どれも見ない人数」を求めることができます。
問題6（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
あるカフェで客200人を対象に、コーヒー、紅茶、オレンジジュースの3種類の飲み物の中で、ふだん飲むものについて調査をおこなった。結果は以下のとおりである。
コーヒー：110票 紅茶：80票 オレンジジュース：60票
なお、コーヒーと紅茶の両方に票を入れたのは35人、紅茶とオレンジジュースの両方に票を入れたのは20人、オレンジジュースとコーヒーの両方に票を入れたのは25人だった。また、3種類すべてに票を入れたのは10人であった。
このとき、3種類の飲み物のうち「1つだけ」票を入れた人は合計で何人か。
選択肢
正解：C
各飲み物について、ほかの飲み物と重複して票を入れた人数を差し引くことで、単独で票を入れた人数を計算する。
たとえば、コーヒーだけを選んだ人数は、全体からコーヒーを含む2種類に票を入れた人数を引いたあと、3つすべてに票を入れた人数を一回足すことで求められる。計算式は、110－35－25＋10＝60（人）となる。
同様に、紅茶だけは80－35－20＋10＝35（人）、ジュースだけは60－20－25＋10＝25（人）である。
これらを合計すると60＋35＋25＝120となるため、答えは120人となる。
文章が長いので、各項目の数値と求めるものは何かという、最低限の必要情報だけを抜き出します。
各項目に単独で入った票数は、「総数−2重−2重＋3重」という式で求められるため、抜き出した数字を型に当てはめて計算していきます。
慣れないうちはベン図を描くことも大切ですが、固定の式に数字を当てはめるように解く習慣をつけると、読み戻しが減ってより安定しますよ。
問題7（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
あるスポーツクラブで、ジム、プール、スタジオの3つの施設の利用状況を調査した。ジムとプールの両方を利用している会員は42人、プールとスタジオの両方を利用している会員は28人、スタジオとジムの両方を利用している会員は35人であった。また、3つの施設すべてを利用している会員は12人であった。
このとき、施設を「ちょうど2つだけ」利用している会員の合計は何人か。
選択肢
正解：A
2つの施設を両方利用する人数には、3つの施設すべてを利用する人数が含まれている。ちょうど2つだけを求めるには、それぞれの組み合わせから3つすべての人数を引く必要がある。
ジムとプールだけ利用：42－12＝30（人） プールとスタジオだけ利用：28－12＝16（人） スタジオとジムだけ利用：35－12＝23（人）
これらを合計すると、30＋16＋23＝69となる。よって、答えは69人。
まず問題文を読んだら、「両方利用している会員」の数と「3つ全部利用している会員」の数、そして「ちょうど2つだけ」という最終的に求めるものを丸で囲いましょう。
ベン図の描き込みは省き、引き算3回＋足し算1回という単純な計算で処理すると素早く解くことができます。
問題8（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある交流会に参加した200人を対象に、SNSのA、B、Cの利用状況について調査をおこなった。SNSのAを利用している人は75人、Bは60人、Cは35人であった。このうち、SNSのCだけを利用している人が20人、いずれのSNSも利用していない人が45人いたとする。
このとき、SNSのAもしくはSNSのBを利用している人は何人か？
選択肢
正解：C
求めたいのは「AもしくはBを利用している人」の人数である。
全体の200人は、以下の3つのグループに分けられる。1つめは、AもしくはBを利用している人。2つめは、Cだけを利用している人。3つめは、何も利用していない人。求めたいのは1つめの「AもしくはBを利用している人」である。
問題文より、2つめは20人、3つめは45人である。これらを合計した65人が「AもBも利用していない人」の総数となる。全体からこの人数を引けば、200－65＝135となる。よって、135人とわかる。
なお、A、B、Cそれぞれの合計人数は今回の計算には使用しない。
求めるのは「AもしくはB」なので「全体の数」「Cだけを利用している人の数」「利用していない人の数」の、3つに情報を絞ることが大切です。
A、B、Cのそれぞれの総数は今回の計算に必要ないということに素早く気付いて、切り捨てることができるかがポイントになります。
問題9（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある店舗の利用者300人を対象に、スマートフォンの決済アプリAとアプリBを利用しているか調査をおこなった。アプリAを利用している人は110人、アプリBを利用している人は90人いた。どちらのアプリも利用していない人が、両方のアプリを利用している人の5倍の人数いたとする。
このとき、両方のアプリを利用している人の人数は何人か？
選択肢
正解：B
求めたい「両方のアプリを利用している人数」をx人と置く。すると、どちらのアプリも利用していない人数は5x人と表せる。
全体の300人は次の式で表すことができる。300＝（アプリAの利用者）＋（アプリBの利用者）－（両方の利用者）＋（どちらも利用していない人）この式に数値を代入すると、300＝110＋90－x＋5xとなる。
これを計算すると300＝200＋4xとなり、100＝4xからx＝25が求められる。
したがって、正解は25人。
このタイプの問題では、問題を読みながら「全体300、A110、B90、無しは5倍、問われているのは両方」と必要な情報を抜き出し、どこをxと置くかをすぐに考えられるようにしましょう。
両方をx人とすると、無しは5x人。300＝110＋90−x＋5xと式が立てられるので、あとは式を整理するだけで求めることができます。
問題10（難易度：★★★☆☆）
問題
次の問いに対する答えとして、最も適切なものを1つ選びなさい。
ある企業の従業員150人のうち、通勤に電車を利用している人は112人、バスを利用している人は68人であった。
電車とバスの両方を利用している人は、最も多くて何人か。
選択肢
正解：C
2つの集合の重なりが最大となるのは、人数の少ないほうの集合が、多いほうの集合の中に完全に含まれるときである。
この問題では、以下の人数が示されている。
電車利用者：112人 バス利用者：68人
バスを利用する68人すべてが、電車も利用していると仮定する。このとき、両方を利用する人は68人となる。これは電車利用者の人数の中に収まっており、矛盾しない。
したがって、最大値は68人である。
「最も多くて」の問題は、「重なりの最大値＝小さいほうの集合の人数」という型を覚えていれば簡単に解くことができます。
全体の数である150人は矛盾の確認に使うだけなので、気を取られないように注意しましょう。
問題11（難易度：★★★☆☆）
問題
次の問いに対する答えとして、最も適切なものを1つ選びなさい。
あるセミナーの参加者120人の男性と女性の比率は11：4で、そのうち有料の会員登録をしている人は80人だった。
会員登録をしていない男性は少なくとも何人いるか。
選択肢
正解：A
まず、男女それぞれの人数を確定させる。
全体の比の合計は11＋4＝15のため、比の1に相当する人数は、120÷15＝8（人）となる。
男性の人数：11×8＝88（人）女性の人数：4×8＝32（人）全体120人のうち、会員は80人なので、会員登録をしていない人は、120－80＝40（人）とわかる。
会員登録をしていない男性を最小にするには、女性32人すべてが会員登録をしていないと仮定すれば良い。
40－32＝8となるため、答えは8人となる。
「少なくとも」の問題でありがちなミスは、「最も多くて」を求める際の「重なりの最大値＝小さいほうの集合の人数」の発想を用いて計算してしまうことです。
「少なくとも」と「最も多くて」はまったくの別物なので、ごっちゃにならないよう注意してください。
問題12（難易度：★★★☆☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある新製品の説明会において、来場者のうち、資料を請求した人は62%、後日の試用を申し込んだ人は44%で、どちらも希望しなかった人は18%であった。
両方とも希望した人が48人であったとき、この説明会の来場者は全部で何人か。
選択肢
正解：C
両方を希望した人の割合を求め、全体の人数を逆算することで求めることができる。
まず、どちらも希望しなかった人（18%）を全体（100%）から引くと、100－18＝82（%）となる。これが「資料か試用の少なくとも一方を希望した人」の割合である。
次に、資料（62%）と試用（44%）を合計した106%から、実質的な割合である82%を引く。106－82＝24（%）が重複する「両方とも希望した人」の割合となる。
全体の24%が48人にあたるため、48÷0.24＝200。よって、答えは200人。
％問題でも基本は同じで、拾う情報を最低限に絞ります。今回であれば、資料62%、試用44%、どちらも無し18%、両方48人という4つの数値です。
情報を絞ることで読む時間は最小に、抜き出した数字を式にスムーズに当てはめるように解くと安定して正解を導き出せますよ。
問題13（難易度：★★★☆☆）
問題
次の資料は、ある通信販売の利用者300人を対象におこなった、満足度調査の結果をまとめたものである。資料を読み、あとの問いに答えなさい。
調査項目と結果の一部は、以下の通りである。
| 調査項目 | 満足 | 不満足 | 合計 |
|---|---|---|---|
| 梱包の状態 | 220人 | 80人 | 300人 |
| 配送スピード | 190人 | 110人 | 300人 |
梱包の状態にも配送スピードにも「満足」と答えた人は150人だったとき、梱包の状態には「満足」で配送スピードには「不満足」と答えた人は何人いるか求めよ。
選択肢
正解：D
まず、梱包の状態に「満足」と答えた人の合計を、表から確認すると220人とわかる。この220人は、配送スピードの評価によって、次の2つのグループに分けられる。
1つ目は、梱包の状態に満足し、かつ、配送スピードにも満足した人。2つ目は、梱包の状態に満足し、かつ、配送スピードには不満足だった人である。
問題文より、1つ目の「両方に満足した人」は150人である。求めたいのは2つ目の人数であるため、梱包の状態に満足した全体の人数から、両方に満足した人数を引くことで求められる。
220-150=70。したがって、答えは70人。
問題14（難易度：★★★★☆）
問題
次の問いに対する答えとして、最も適切なものを1つ選びなさい。
ある試験の受験者210人のうち、ＡグループとＢグループの比率は2：5であった。
試験の合格者が140人だったとき、不合格となったＢグループの受験者は少なくとも何人いるか。
選択肢
正解：A
まず、各グループの人数を求める。
比の合計は7（2＋5）のため、比の1に相当する人数は、210÷7＝30（人）となる。Ａグループの人数：2×30＝60（人）Ｂグループの人数：5×30＝150（人）全体210人のうち、合格者は140人なので、不合格者は、210－140＝70（人）となる。
Ｂグループの不合格者を最小にするには、Ａグループの受験者60人すべてが不合格であったと仮定すれば良い。不合格者の総数70人からＡグループの60人を引くと、70－60＝10となり、答えは10人と求められる。
比を用いた「少なくとも」の問題を解くコツは、「比を元に人数を確定する→不合格者の総数を求める→最小を求める」という手順を固定化することです。
ありがちなミスは、「少なくとも」を見落として下限ではない数を答えてしまうことです。「少なくとも」「最も多くて」といった、重要な条件は見落とさないよう注意しましょう。
問題15（難易度：★★★★☆）
問題
次の問いについて、当てはまるものを選択肢の中から1つ選びなさい。
ある企業の従業員を対象に健康診断の結果を分析したところ、血圧の再検査が必要な人は68%、血糖値の再検査が必要な人は54%であった。また、いずれの項目も再検査の必要がなかった人は13%であった。
両方の項目で再検査が必要となった従業員が105人であったとき、この調査の対象となった従業員は全部で何人か。
選択肢
正解：C
まず、全体の100%から、どちらの項目にも該当しなかった13%を引く。100－13＝87（%）が、少なくとも一方の項目で再検査が必要な人の割合となる。
次に、血圧（68%）と血糖値（54%）の合計である122%から、先ほどの87%を引く。122－87＝35（%）が重複している「両方の項目で再検査が必要な人」の割合だとわかる。
問題文より、この35%が105人にあたるため、全体の人数は105÷0.35＝300と計算することで求められる。したがって、答えは300人。
割合を用いた問題は「合計−少なくとも一方＝重複」の型を覚えておくとスムーズに解くことができます。
少なくとも一方＝100−13＝87%、全体は68＋54＝122%なので、この差35%が重複の割合になります。
105人が35%なので、105÷0.35で全体の数を求めることができます。
練習問題が解けたら、次はSPI模試に挑戦して実力をチェックしてみましょう。
SPI「集合」を対策する際のポイント
SPIの非言語に関する記事
◇非言語の対策
SPI非言語は対策すれば怖くない！ 出題傾向や例題を徹底解説
SPIに関する記事
◇解答時間
SPIの解答時間を受検方式別に解説！ 時間切れを防ぐコツ10選も
◇勉強法
効率抜群なSPIの勉強法｜出題形式と頻出問題を踏まえた対策を伝授
◇勉強時間
SPIの勉強時間をプロが解説！ おすすめの進め方や重点ポイントも
集合以外の練習問題も解いてみよう！
SPIは多くの分野に分かれています。練習問題を繰り返し解いて、苦手を攻略しましょう。
各分野の問題が解けたら、最後にSPI模試に挑戦してみましょう。
執筆・編集 PORTキャリア編集部
明日から使える就活ノウハウ情報をテーマに、履歴書・志望動機といった書類の作成方法や面接やグループワークなどの選考対策の方法など、多様な選択肢や答えを提示することで、一人ひとりの就活生の意思決定に役立つことを目指しています。 国家資格を保有するキャリアコンサルタントや、現役キャリアアドバイザーら専門家監修のもと、最高品質の記事を配信しています。
＞ コンテンツポリシー
記事の編集責任者 熊野 公俊 Kumano Masatoshi
高校卒業後、航空自衛隊に入隊。4年間の在籍後、22歳で都内の大学に入学し、心理学・教育学を学ぶ。卒業後は人材サービスを展開するパソナで、人材派遣営業やグローバル人材の採用支援、女性活躍推進事業に従事。NPO（非営利団体）での勤務を経て、「PORTキャリア」を運営するポートに入社。キャリアアドバイザーとして年間400人と面談し、延べ2500人にも及ぶ学生を支援。2020年、厚生労働大臣認定のキャリアコンサルタント養成講習であるGCDF-Japan（キャリアカウンセラートレーニングプログラム）を修了
アドバイザーからワンポイントアドバイス「集合」はSPIで最頻出！ 念入りな対策が必須
ジョブカード作成アドバイザー
田中 直香
プロフィールを見る「式だけで解く」習慣とタイムアタック練習で時短しよう
SPI集合の攻略のコツは、「ベン図」を卒業し「式だけで解く」スタイルへ移行することです。いちいち図を描くとタイムロスになるため、A+B-重複=全体などの決まった公式に、問題文の数字を機械的に当てはめる練習をしてください。
出題頻度は極めて高いため、対策時間は優先的に割くべきです。「1問1分」を目安に解き切るタイムアタック練習を1日15分を目安に取り組むようにしましょう。
対策すべきパターンは2つ！
重点的に対策すべきは「3つの集合」と「最大・最小」です。これらは難易度が高く、正解できるとライバルに差をつけることができます。
数学への苦手意識が強い人は、まずは「2つの集合」の基本計算だけを完璧に仕上げてください。基礎を固めるだけでも十分な得点源になります。
問題文に丸を付けながら解く習慣が攻略のカギ
多くの人が陥るミスは、「Aを利用している人（全体）」と「Aだけを利用している人（単独）」の読み違えです。問題文の「だけ」や「のみ」という重要な言葉に丸をつける癖をつけると、計算ミス以外の「もったいない失点」は激減します。